Question

【题目】如图，平面直角坐标系中，直线AB：交y轴于点A(0，1)，交x轴于点B．直线x=1交AB于点D，交x轴于点E，P是直线x=1上一动点，且在点D的上方，设P(1，n)．

(1)求直线AB的解析式和点B的坐标；

(2)求△ABP的面积(用含n的代数式表示)；

(3)当S△ABP=2时，以PB为边在第一象限作等腰直角三角形BPC，求出点C的坐标．

Answer 1

【答案】(1) AB的解析式是y=-x+1．点B（3，0）．(2)n-1；(3) （3，4）或（5，2）或（3，2）．

【解析】

试题（1）把A的坐标代入直线AB的解析式，即可求得b的值，然后在解析式中，令y=0，求得x的值，即可求得B的坐标；

（2）过点A作AM⊥PD，垂足为M，求得AM的长，即可求得△BPD和△PAB的面积，二者的和即可求得；

（3）当S△ABP=2时，n-1=2，解得n=2，则∠OBP=45°，然后分A、B、P分别是直角顶点求解．

试题解析：（1）∵y=-x+b经过A（0，1），

∴b=1，

∴直线AB的解析式是y=-x+1．

当y=0时，0=-x+1，解得x=3，

∴点B（3，0）．

（2）过点A作AM⊥PD，垂足为M，则有AM=1，

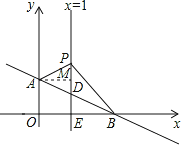
∵x=1时，y=-x+1=，P在点D的上方，

∴PD=n-，S△APD=PDAM=×1×(n-)=n-

由点B（3，0），可知点B到直线x=1的距离为2，即△BDP的边PD上的高长为2，

∴S△BPD=PD×2=n-，

∴S△PAB=S△APD+S△BPD=n-+n-=n-1；

（3）当S△ABP=2时，n-1=2，解得n=2，

∴点P（1，2）．

∵E（1，0），

∴PE=BE=2，

∴∠EPB=∠EBP=45°．

第1种情况，如图1，∠CPB=90°，BP=PC，过点C作CN⊥直线x=1于点N．

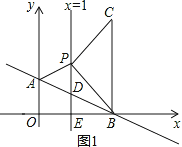
∵∠CPB=90°，∠EPB=45°，

∴∠NPC=∠EPB=45°．

又∵∠CNP=∠PEB=90°，BP=PC，

∴△CNP≌△BEP，

∴PN=NC=EB=PE=2，

∴NE=NP+PE=2+2=4，

∴C（3，4）．

第2种情况，如图2∠PBC=90°，BP=BC，

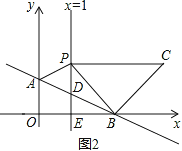
过点C作CF⊥x轴于点F．

∵∠PBC=90°，∠EBP=45°，

∴∠CBF=∠PBE=45°．

又∵∠CFB=∠PEB=90°，BC=BP，

∴△CBF≌△PBE．

∴BF=CF=PE=EB=2，

∴OF=OB+BF=3+2=5，

∴C（5，2）．

第3种情况，如图3，∠PCB=90°，CP=EB，

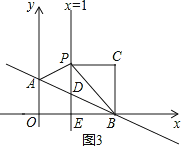
∴∠CPB=∠EBP=45°，

在△PCB和△PEB中，

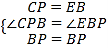
∴△PCB≌△PEB（SAS），

∴PC=CB=PE=EB=2，

∴C（3，2）．

∴以PB为边在第一象限作等腰直角三角形BPC，点C的坐标是（3，4）或（5，2）或（3，2）．