��Ŀ����
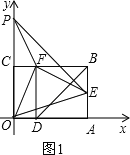
����Ŀ����ͼ,�Ծ���OABC�Ķ���OΪԭ��,OA���ڵ�ֱ��Ϊx��,OC���ڵ�ֱ��Ϊy��,����ƽ��ֱ������ϵ.��֪OA=3,OC=2,��E��AB���е�,��OA��ȡһ��D,����BDA��BD���ۣ�ʹ��A����BC���ϵĵ�F����
��1��ֱ��д����E��F�����ꣻ
��2���趥��ΪF�������߽�y���������ڵ�P,���Ե�E��F��PΪ������������ǵ��������Σ���������ߵĽ���ʽ��
��3����x�ᡢy�����Ƿ�ֱ���ڵ�M��N,ʹ���ı���MNFE���ܳ���С���������,����ܳ�����Сֵ�����������,��˵�����ɣ�

���𰸡���1��E(3��1),F(1��2);��2��![]() ����3�����ڣ���С�ı���MNFE���ܳ���Сֵ��5+
����3�����ڣ���С�ı���MNFE���ܳ���Сֵ��5+![]() ��
��
����������������1����BDA��BD���ۣ�ʹ��A����BC���ϵĵ�F��������֪���ı���ADFB�������Σ����BF=AB=OC=2����CF=3-2=1�����E��F������Ϳ����������2������ΪF��������ݵ�һ�ʿ�������ǣ�1��2������������ߵĽ���ʽ������Ϊy=a��x-1��2+2���Ե�E��F��PΪ������������ǵ��������Σ�Ӧ��EF�����͵ױ���������������ۣ�
����EF������EF=PFʱ����֪E��F�������������EF�ij�����P��������ǣ�0��n�������ݹ��ɶ����Ϳ������n��ֵ���õ�P�����꣮��EF������EF=EPʱ�������ж�E��y�����̾�����EF�Ĵ�С��ϵ��ֻ�е�EF����E��y��ľ��룬P�Ŵ��ڣ�
����EF�ǵױ�ʱ��EP=FP�����ݹ��ɶ����Ϳ��Եõ�����n�ķ��̣��Ϳ��Խ��n��ֵ��
��3������E����x��ĶԳƵ�E��������F����y��ĶԳƵ�F��������E��F�����ֱ���x�ᡢy�ύ�ڵ�M��N�����M��N��������㣮����߶�E��F���ij��ȣ������ı���MNFE���ܳ�����Сֵ��
���������(1)E(3,1);F(1,2).
(2)��Rt��EBF��,��B=90����EF=![]()
���P������Ϊ(0,n)������n>0���߶���F(1,2)��
���������߽���ʽΪy=a(x1) ![]() +2(a��0).
+2(a��0).
����ͼ1��
 ��EF=PFʱ,
��EF=PFʱ, ![]() ��
��
��![]() .
.
���![]() (��ȥ);
(��ȥ); ![]() .
.
��P(0,4).
��4=a(01) ![]() +2.
+2.
���a=2.
�������ߵĽ���ʽΪy=2(x1) ![]() +2
+2
����ͼ2��
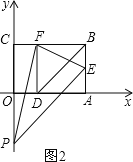
��EP=FPʱ,EP![]() =FP
=FP![]() ����(2n)
����(2n) ![]() +1=(1n)
+1=(1n) ![]() +9.���n=
+9.���n=![]() (��ȥ)
(��ȥ)
�۵�EF=EPʱ,EP=![]() <3��������������ڡ�
<3��������������ڡ�
��������,���������������߽���ʽ��y=2(x1) ![]() +2.
+2.
(3)���ڵ�M,N,ʹ���ı���MNFE���ܳ���С��
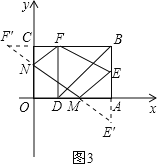
��ͼ3,����E����x��ĶԳƵ�E��,����F����y��ĶԳƵ�F�䣬
����E��F�����ֱ���x�ᡢy�ύ�ڵ�M��N�����M��N��������㡣
��E��(3,1),F��(1,2),NF=NF��,ME=ME��.��BF��=4,BE��=3.
��FN+NM+ME=F��N+NM+ME��=E��F��=![]() .
.
�֡�EF=![]() ��
��
��FN+MN+ME+EF=5+![]() ,��ʱ�ı���MNFE���ܳ���Сֵ��5+
,��ʱ�ı���MNFE���ܳ���Сֵ��5+![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij����ӵ�пͷ�100�䣬��Ӫ�з��֣�ÿ����ס�Ŀͷ���y(��)�뷿��x(Ԫ)(180��x��300)����һ�κ�����ϵ�����ֶ�Ӧֵ���±���
x(Ԫ) | 180 | 260 | 280 | 300 |
y(��) | 100 | 60 | 50 | 40 |
(1)��y��x֮��ĺ�������ʽ��
(2)��֪ÿ����ס�Ŀͷ�������ÿ����֧�����ַ���100Ԫ��ÿ����õĿͷ�������ÿ����֧�����ַ���60Ԫ��������Ϊ����Ԫʱ�����ݵ��������������������(���ݵ�������=���շ�������-����֧��)


