题目内容
【题目】在△ABC中,∠B和∠C的平分线交于点I,边AB和AC的垂直平分线交于点O,若∠BIC=90°+![]() θ,则∠BOC=( )
θ,则∠BOC=( )
A.90°﹣![]() θB.2θC.180°﹣θD.以上答案都不对
θB.2θC.180°﹣θD.以上答案都不对
【答案】B
【解析】
根据角平分线的性质可得∠A=θ,再根据线段垂直平分线的性质和三角形内角和定理即可推出∠BOC.
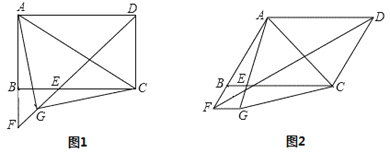
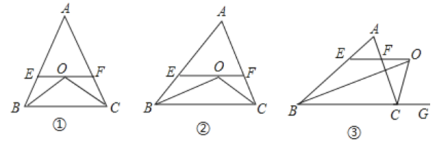
解:如图,
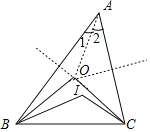
∵∠B和∠C的平分线交于点I,
∴∠IBC=![]() ∠ABC,∠ICB=
∠ABC,∠ICB=![]() ∠ACB,
∠ACB,
∠BIC=180°﹣(∠IBC+∠ICB)
=180°﹣![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°﹣![]() (180°﹣∠BAC)
(180°﹣∠BAC)
=180°﹣90°+![]() ∠BAC
∠BAC
=90°+![]() ∠BAC,
∠BAC,
∵∠BIC=90°+![]() θ,
θ,
∴∠BAC=θ.
∵AB和AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠1=∠OBA,∠2=∠OCA,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC﹣∠1+∠ACB﹣∠2)
=180°﹣(180°﹣∠BAC﹣∠1﹣∠2)
=∠BAC+∠1+∠2
=2∠BAC
=2θ.
故选:B.

练习册系列答案
相关题目
【题目】某商场出售一批进价为2元的贺卡,在营运中发现此商品的日销价x(单位:元)与销售量y(单位:张)之间有如下关系:
x/元 | 3 | 4 | 5 | 6 |
y/张 | 20 | 15 | 12 | 10 |
(1)猜测并确定y与x的函数关系式.
(2)当日销售单价为10元时,贺卡的日销售量是多少张?
(3)设此卡的利润为W元,试求出W与x之间的函数关系式,若物价部门规定此卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大并求出最大的利润.