��Ŀ����
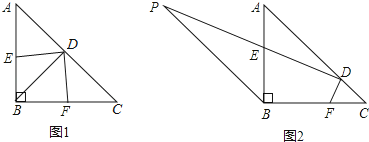
����Ŀ����ͼ�٣���ABC�У�AB=AC����B����C��ƽ���߽���O�㣬��O����EF��BC��AB��AC��E��F.
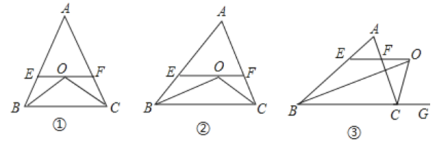
(1)ͼ�����м�������������?����:EF��BE��CF֮���������Ĺ�ϵ.
(2)��ͼ��,��AB��AC�������������䣬ͼ�л��е�����������?����У��ֱ�ָ������.�ڵ�(1)����EF��BE��CF��Ĺ�ϵ��������?
(3)��ͼ�ۣ�����ABC�С�B��ƽ����BO�����������ƽ����CO����O����O����OE��BC��AB��E����AC��F.��ʱͼ�л��е�����������?EF��BE��CF��ϵ�����?˵���������.
���𰸡���1����AEF����OEB����OFC����OBC����ABC��5����EF=BE+FC����2���У���EOB����FOC�����ڣ���3���У�EF=BE-FC��
��������
��1����AB=AC���ɵá�ABC=��ACB������֪OB��OC�ֱ�ƽ�֡�ABC����ACB���ʡ�EBO=��OBC=��FCO=��OCB������EF��BC���ɵã���OEB=��OBC=��EBO����FOC=��FCO=��BCO���ɴ˿ɵó��ĵ����������У���AEF����OEB����OFC����OBC����ABC��
��֪�ˡ�EOB�͡�FOC�ǵ��������Σ���EO=BE��OF=FC����EF=BE+FC��
��2���ɣ�1����֤�����̿�֪����֤��OEB����OFC�ǵ��������εĹ����У���AB=AC������û�й�ϵ�������������������λ����������ԣ�1���еó���EF=BE+FC�Ľ����Գ�����
��3��˼·�루2����ͬ��ֻ������������EF=BE-FC��
�⣺��1��ͼ���ǵ��������ε��У���AEF����OEB����OFC����OBC����ABC��
EF��BE��FC�Ĺ�ϵ��EF=BE+FC���������£�
��AB=AC��
���ACB=��ABC����ABC�ǵ��������Σ�
��BO��CO�ֱ�ƽ�֡�ABC�͡�ACB��
���ABO=��OBC=![]() ��ABC����OCB=��ACO=
��ABC����OCB=��ACO=![]() ��ACB��
��ACB��
��EF��BC��
���EOB=��OBC����FOC=��OCB��
���ABO=��OBC=��EOB=��OCB=��FOC=��FCO��
���EOB����OBC����FOC���ǵ��������Σ�
��EF��BC��
���AEF=��ABC����AFE=��ACB��
���AEF=��AFE��
���AEF�ǵ��������Σ�
��OB��OCƽ�֡�ABC����ACB��
���ABO=��OBC����ACO=��OCB��
��EF��BC��
���EOB=��OBC=��EBO����FOC=��OCB=��FCO��
��EO=EB��FO=FC��
��EF=EO+OF=BE+CF��
��2����AB��ACʱ����EOB����FOC��Ϊ���������Σ���1���Ľ�����Ȼ������
��OB��OCƽ�֡�ABC����ACB��
���ABO=��OBC����ACO=��OCB��
��EF��BC��
���EOB=��OBC=��EBO����FOC=��OCB=��FCO��
��EO=EB��FO=FC��
��EF=EO+OF=BE+CF��
��3����EOB�͡�FOC���ǵ��������Σ�EF=BE-FC���������£�
ͬ��1����֤�á�EOB�ǵ��������Σ�
��EO��BC��
���FOC=��OCG��
��OCƽ�֡�ACG��
���ACO=��FOC=��OCG��
��FO=FC���ʡ�FOC�ǵ��������Σ�
��EF=EO-FO=BE-FC��

 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�