题目内容
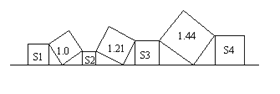
【题目】如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4= .
【答案】2.44
【解析】
由条件可以得出AC=CF=1,FH=LH=1.1,PR=SR=1.2.由正方形的性质可以得出∠ACB=∠CED,∠FHG=∠HLM,∠PRN=∠RST,就可以得出△ABC≌△CDE,△FGH≌△HML,△PNR≌△RTS,就可以得出AB=CD,BC=DE,FG=HM,GH=ML,PN=RT,NR=ST,由勾股定理就可以AB2+BC2=AC2,FG2+GH2=FH2,NP2+NR2=PR2,由正方形的面积公式就可以得出结论.
解:如图,

∵斜放置的三个正方形的面积分别为1,1.21,1.44,
∴AC=CF=1,FH=LH=1.1,PR=SR=1.2.∠ACD=∠FHL=∠PRS=90°,
∴∠ACB=∠CED,∠FHG=∠HLM,∠PRN=∠RST,
∴△ABC≌△CDE,△FGH≌△HML,△PNR≌△RTS,
∴AB=CD,BC=DE,FG=HM,GH=ML,PN=RT,NR=ST,
由勾股定理,得
AB2+BC2=AC2,FG2+GH2=FH2,NP2+NR2=PR2,
∴S1+S2=1.0,S2+S3=1.21,S3+S4=1.44,
∴S1+S2+S2+S3+S3+S4=1+1.21+1.44=3.65,
∴S1+2S2+2S3+S4=3.65.
∴S1+S2+S3+S4=2.44.
故答案为:2.44.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目