题目内容
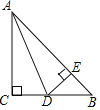
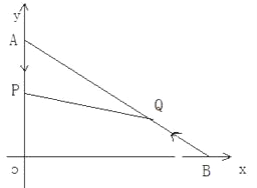
【题目】如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒.
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
【答案】(1)y=-![]() x+12;(2)
x+12;(2)![]() ,
,![]() ;(3)2,8;(4)5,20.
;(3)2,8;(4)5,20.
【解析】
试题(1)设直线AB的解析式为y=kx+b,解得k,b即可;
(2)由AO=6,BO=8得AB=10,①当∠APQ=∠AOB时,△APQ∽△AOB利用其对应边成比例解t.②当∠AQP=∠AOB时,△AQP∽△AOB利用其对应边成比例解得t.
(3)根据△APQ的面积为![]() ,求出t的值.
,求出t的值.
(3)过点O作QE⊥AO于点E,利用t表示出△APQ的面积,利用函数的性质即可求解.
试题解析:(1)设直线AB的解析式为y=kx+b,
由题意,得![]()
解得: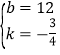
所以,直线AB的解析式为y=-![]() x+12;
x+12;
(2)由AO=12,BO=16得AB=20,
所以AP=t,AQ=20-2t,
①当∠APQ=∠AOB时,△APQ∽△AOB.
所以![]() ,
,
解得t=![]() (秒),
(秒),
②当∠AQP=∠AOB时,△AQP∽△AOB.
所以![]() ,
,
解得t=![]() (秒);
(秒);
∴当t为![]() 秒或
秒或![]() 秒时,△APQ与△AOB相似;
秒时,△APQ与△AOB相似;
(3)过Q点作QE⊥Y轴于点E,
由△AQE∽△AOB知:![]()
即:![]()
解得:QE=![]()
又S△APQ=![]()
解得:![]() ,
,![]()
(4)∵QE=![]()
∴S△APQ=![]() APQE=
APQE=![]() t(
t(![]() )=-
)=-![]() t2+8t=-
t2+8t=-![]() (t-5)2+20
(t-5)2+20
∴当t=5时,△APQ的面积最大,最大面积是20个平方单位.
考点: 一次函数综合题.

练习册系列答案
相关题目