题目内容
【题目】抛物线y=–![]() x2+bx+c经过点A(3
x2+bx+c经过点A(3![]() ,0)和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.
,0)和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.
(1)求抛物线的解析式;
(2)连接AB、AC、BC,求△ABC的面积.

【答案】(1)![]() (2)3
(2)3![]()
【解析】
(1)将点A(3![]() ,0)和点B(0,3),代入函数解析式中得到关于b,c的二元一次方程组,然后求解即可;
,0)和点B(0,3),代入函数解析式中得到关于b,c的二元一次方程组,然后求解即可;
(2)如图,首先利用抛物线对称轴与(1)得到的解析式求出顶点C的坐标,再求出线段AB所在直线的函数解析式,从而求出AB与对称轴交点D的坐标,然后过点B作BF⊥l于点F,则有S△ABC=S△BCD+S△ACD=![]() CDBF+
CDBF+![]() CDAE,求解即可得到答案.
CDAE,求解即可得到答案.
(1)∵抛物线![]() 经过A(
经过A(![]() ,0)、B(0,3),
,0)、B(0,3),
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)由(1)得抛物线对称轴为直线x=![]() ,
,
把x=![]() 代入,
代入,![]() ,得y=4,
,得y=4,
则点C坐标为(![]() ,4);
,4);
设线段AB所在直线为:y=kx+b,
∵线段AB所在直线经过点A(![]() ,0)、B(0,3),
,0)、B(0,3),
∴![]() ,解得
,解得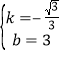 ;
;
令抛物线的对称轴l与直线AB交于点D,
∴设点D的坐标为(![]() ,m),
,m),
将点D(![]() ,m)代入
,m)代入![]() ,解得m=2;
,解得m=2;
∴点D坐标为(![]() ,2),
,2),
∴CD=CE–DE=2;
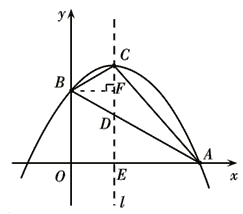
过点B作BF⊥l于点F,∴BF=OE=![]() ;
;
∵BF+AE=OE+AE=OA=3![]() ,
,
∴S△ABC=S△BCD+S△ACD=![]() CDBF+
CDBF+![]() CDAE
CDAE
∴S△ABC=![]() CD(BF+AE)=
CD(BF+AE)=![]() ×2×
×2×![]() =3
=3![]() .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目