题目内容

【题目】如图，在等腰三角形纸片ABC中，AB＝AC＝5，BC＝6，沿底边BC上的高AD剪成两个三角形，用这两个三角形拼成平行四边形，则拼成的各种平行四边形中，其中最长的对角线的值为_____．

【答案】

【解析】

利用等腰三角形的性质，进而重新组合得出平行四边形，进而利用勾股定理求出对角线的长．

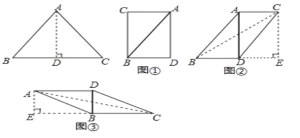
如图：过点A作AD⊥BC于点D，
∵△ABC边AB=AC=5，BC=6，
∴BD=DC=3，
∴AD=4，
如图①所示：
可得四边形ACBD是矩形，则其对角线长为：5，
如图②所示：AD=4，
连接BC，过点C作CE⊥BD于点E，
则EC=4，BE=2BD=6，
则BC=2，
如图③所示：BD=3，
由题意可得：AE=3，EC=2BE=8，
故AC=
故答案为：.

练习册系列答案
相关题目

【题目】（1）①如图①的内角的平分线与内角的平分线相交于点，请探究与的关系，并说明理由．

②如图②，的内角的平分线与外角的平分线相交于点，请探究与的关系，并说明理由．

（2）如图③④，四边形中，设，， 为四边形的内角与外角的平分线所在直线相交而行成的锐角．请利用（1）中的结论完成下列问题：

①如图③，求的度数．（用 的代数式表示）

②如图④，将四边形沿着直线翻折得到四边形，为延长线上一点，连接，与的角平分线交于点，求与的数量关系．

【题目】盒中有x枚黑棋和y枚白棋，这些棋除颜色外无其他差别．

（1）从盒中随机取出一枚棋子，如果它是黑棋的概率是，写出表示x和y关系的表达式．

（2）往盒中再放进10枚黑棋，取得黑棋的概率变为，求x和y的值．

【题目】(9分)如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A(－3，2)，B(0，4)，C(0，2)．

(1)将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；平移△ABC，若A的对应点A2的坐标为(0，4)，画出平移后对应的△A2B2C2；

(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标．

【题目】如图，已知抛物线过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．

（1）求抛物线的解析式；

（2）设点M（1，m），当MB+MD的值最小时，求m的值；

（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；

（4）若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．

【题目】图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：

（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：　 　；

（2）仔细观察，在图2中“8字形”的个数：　 　个；

（3）图2中，当∠D＝50度，∠B＝40度时，求∠P的度数．

（4）图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．（直接写出结果，不必证明）．

【题目】如图，在平面直角坐标系中，直线l1：分别与x轴、y轴交于点B、C，且与直线l2：交于点A．

（1）求出点A的坐标

（2）若D是线段OA上的点，且△COD的面积为12，求直线CD的解析式

（3）在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点P的坐标；若不存在，请说明理由．

【题目】阅读可以增进人们的知识也能陶治人们的情操。我们要多阅读，多阅读有营养的书。因此我校对学生的课外阅读时间进行了抽样调查，将收集的数据分成A、B、C、D、E五组进行整理，整理后的数据如下表（表中信息不完整）。图1和图2是根据整理后的数据绘制的两幅不完整的统计图.

阅读时间分组统计表

组别

阅读时间x（h）

人数

A

a

B

100

C

b

D

140

E

c

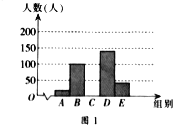
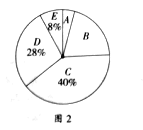
请结合以上信息解答下列问题

（1）求a，b，c的值；

（2）补全图1所对应的统计图；

（3）估计全校课外阅读时间在20h以下（不含20h）的学生所占百分比.

【题目】抛物线y=–x2+bx+c经过点A（3，0）和点B（0，3），且这个抛物线的对称轴为直线l，顶点为C．

（1）求抛物线的解析式；

（2）连接AB、AC、BC，求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网