题目内容
【题目】已知抛物线y=x2-2x-8.
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积.
【答案】(1)△=36 >0;(2)△ABP面积为27
【解析】
(1)根据b2﹣4ac与零的关系即可判断出二次函数y=x2﹣2x﹣8的图象与x轴交点的个数;
(2)先求出AB的长,然后配方得到抛物线的顶点坐标,根据三角形面积公式即可得出结论.
(1)△=(-2)2-4×1×(-8)=4+32=36>0.
故抛物线y=x2﹣2x﹣8与x轴有两个交点.
(2)令y=0,得:x2﹣2x﹣8=0,解得:x1=﹣2,x2=4,∴A(﹣2,0),B(4,0),故AB=6.由y=x2﹣2x﹣8=x2﹣2x+1﹣9=(x﹣1)2﹣9,故P点坐标为(1,﹣9);
过P作PC⊥x轴于C,则PC=9,∴S△ABP![]() ABPC
ABPC![]() 6×9=27.
6×9=27.

练习册系列答案
相关题目
【题目】阅读可以增进人们的知识也能陶治人们的情操。我们要多阅读,多阅读有营养的书。因此我校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,整理后的数据如下表(表中信息不完整)。图1和图2是根据整理后的数据绘制的两幅不完整的统计图.
阅读时间分组统计表 | ||
组别 | 阅读时间x(h) | 人数 |
A |
| a |
B |
| 100 |
C |
| b |
D |
| 140 |
E |
| c |
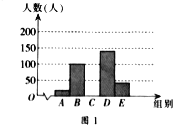
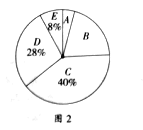
请结合以上信息解答下列问题
(1)求a,b,c的值;
(2)补全图1所对应的统计图;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.