题目内容
【题目】证明：有两边和第三边上的中线对应相等的两个三角形全等。
【答案】见解析.
【解析】
先据题画出图形，写出已知与求证，再分别延长AM到P，使MP=AM，DN到Q，使NQ=DN，连接BP，EQ，用SAS可证△BMP≌△CMA，得∠P=∠CAM，BP=AC，同理可证得∠Q=∠FDN，EQ=DF，于是由SSS可证△ABP≌△DEQ，得∠BAP=∠EDQ，∴∠BAC=∠EDF，再用SAS即可证得结论.
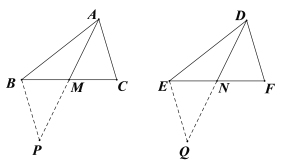
已知：如图，△ABC与△DEF中，AB=DE，AC=DF，BC、EF边上的中线AM=DN.
求证：△ABC≌△DEF.
证明：分别延长AM到P，使MP=AM，DN到Q，使NQ=DN，连接BP，EQ.
∵AM=DN，∴AP=DQ，
∵M是BC的中点，∴BM=CM，
又∵∠BMP=∠CMA，
∴△BMP≌△CMA（SAS），
∴∠P=∠CAM，BP=AC，
同理可证△QEN≌△DFN，
∴∠Q=∠FDN，EQ=DF，
∵AC=DF，∴BP=EQ，
在△ABP和△DEQ中，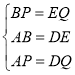
，
∴△ABP≌△DEQ（SSS）.
∴∠BAP=∠EDQ，
∴∠BAC=∠EDF，
又AB=DE，AC=DF，
∴△ABC≌△DEF（SAS）.
即两边和第三边上的中线对应相等的两个三角形全等.
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
