题目内容
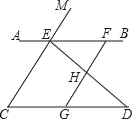
【题目】如图,AB是公园的一圆桌的主视图,MN表示该桌面在路灯下的影子,CD则表示一个圆形的凳子.
(1)请在图中标出路灯O的位置,并画出CD的影子PQ;
(2)若桌面直径与桌面距地面的距离为1.2 m,测得影子的最大跨度MN为2 m,求路灯O与地面的距离.
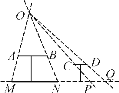
【答案】(1)画图见解析;(2)路灯O与地面的距离为3 m.
【解析】
(1)延长MA、NB,它们的交点即为路灯O的位置,然后再连结OC、OD,并延长交地面与P、Q点,则PQ为CD的影子;
(2)作OF⊥MN交AB于E,如图,AB=1.2m,EF=1.2m,MN=2m,证明△OAB∽△OMN,利用相似比计算出OF即可得到路灯O与地面的距离.
(1)如图所示,线段PQ即为所求.
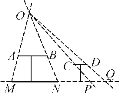
(2) ∵AB∥MN,
∴△OAB∽△OMN,
∴AB:MN=OE:OF,即1.2:2=(OF-1.2):OF,
解得OF=3(m).

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目