题目内容
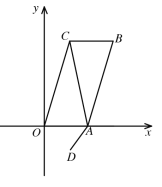
【题目】如图,在平面直角坐标系xOy中,O为原点,点A、C 的坐标分别为(2,0)、(1,3![]() ),将△AOC绕AC的中点旋转180°,点O落到点B的位置,D的坐标为(1,-
),将△AOC绕AC的中点旋转180°,点O落到点B的位置,D的坐标为(1,-![]() ).若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,则点P的坐标为_________.
).若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,则点P的坐标为_________.
【答案】(-1,0)或(1,0)或(3,0)
【解析】
设P点坐标为(a,0),另一个顶点为Q,坐标为(0,b),分三种情况讨论,根据平行四边形对角线互相平分,则两条对角线的中点相同,利用中点坐标公式建立方程求出a即可得到P点坐标.
设P点坐标为(a,0),另一个顶点为Q,坐标为(0,b),分三种情况讨论:
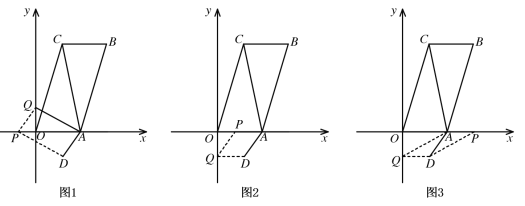
①如图1,当AP、DQ为对角线时,
∵A(2,0),D (1,-![]() ),由平行四边形对角线互相平分的性质和中点坐标公式可得,
),由平行四边形对角线互相平分的性质和中点坐标公式可得,
![]() ,解得
,解得![]() ,
,
∴P点坐标为(-1,0)
②如图2,当AQ、PD为对角线时,
同理可得![]() ,解得
,解得![]()
∴P点坐标为(1,0)
③如图3,当AD、PQ为对角线时,
同理可得![]() ,解得
,解得![]()
∴P点坐标为(3,0)
综上可得P点坐标为(-1,0)或(1,0)或(3,0)

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目