题目内容
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),
重合),![]() ,
,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,则线段
,则线段![]() 的最大值为________.
的最大值为________.

【答案】![]()
【解析】
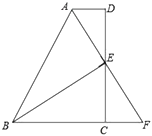
如图,过点A作AG⊥BC于G,根据等腰三角形的性质得BG=CG,再利用余弦的定义计算出BG=8,则BC=2GB=16.设BD=x,则CD=16-x,证明△ABD∽△DCE,利用相似三角形的性质可得CE=![]() ,再利用二次函数的性质求CE的最大值即可.
,再利用二次函数的性质求CE的最大值即可.
过点A作AG⊥BC于G,

∵AB=AC,
∴BG=CG,
∵∠ADE=∠B=α,
∴cosB=![]() =
=![]()
![]() ,
,
∴BG=8,
∴BC=2GB=16.
设BD=x,则CD=16-x,
∵∠ADC=∠B+∠BAD,即∠ADE+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
∵∠C=∠B,
∴△ABD∽△DCE,
∴![]() ,即
,即![]() ,
,
∴CE=![]() ,
,
∴当x=8时,EC有最大值,最大值为6.4.
故答案为:6.4.

练习册系列答案
相关题目