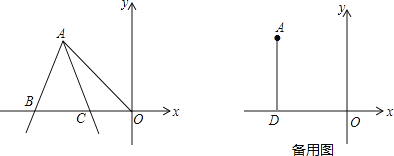题目内容
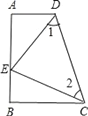
【题目】如图![]() ,以
,以![]() 边
边![]() 和
和![]() 为边作等边
为边作等边![]() 和
和![]() ,连接
,连接![]() ,
,![]() ,
,
![]() 判断
判断![]() 与
与![]() 的数量关系,并求
的数量关系,并求![]() 与
与![]() 的夹角
的夹角![]() 的度数;
的度数;
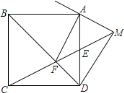
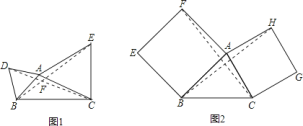
![]() 继续探索,如图
继续探索,如图![]() ,以
,以![]() 的
的![]() 和
和![]() 为边作正方形
为边作正方形![]() 和
和![]() ,连接
,连接![]() 、
、![]() ,判断
,判断![]() 和
和![]() 的数量关系,并求出此时
的数量关系,并求出此时![]() 与
与![]() 的夹角;
的夹角;
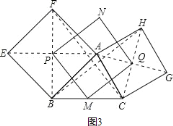
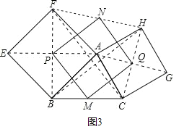
![]() 如图
如图![]() 中
中![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别是正方形的中心,顺次连接
分别是正方形的中心,顺次连接![]() ,判断四边形
,判断四边形![]() 的形状并证明.
的形状并证明.
【答案】(1)![]() ,
,![]() 的度数为
的度数为![]() ;(2)
;(2)![]() 且
且![]() 与
与![]() 的夹角为
的夹角为![]() ;(3) 四边形
;(3) 四边形![]() 为正方形,理由详见解析.
为正方形,理由详见解析.
【解析】
(1)根据等边三角形的性质可得AB=AD,AE=AC,∠BAD=∠CAE=60°,再求出∠BAE=∠DAC,然后利用“边角边”证明△ABE和△ADC全等,根据全等三角形对应边相等可得BE=DC,全等三角形对应角相等可得∠AEB=∠ACD,然后∠FEC+∠FCE=120°,再根据三角形内角和定理计算即可得解;(2)根据正方形的性质可得AB=AF,AC=AH,∠BAF=∠CAH=90°,再求出∠BAH=∠CAF,然后利用“边角边”证明△ABH和△AFC全等,根据全等三角形对应边相等可得BH=FC,全等三角形对应角相等可得∠AFC=∠ABH,然后∠EFC+∠EBH=180°,设BH、CF相交于点G,再根据四边形的内角和定理计算即可求出∠BGF=90°,根据垂线的定义即可得证;根据正方形的对角线互相平分可得点P、Q分别是BF、CH的中点,再根据三角形的中位线平行于第三边并且等于第三边的一半可得PN∥BH,PN=![]() BH,MQ∥BH,MQ=
BH,MQ∥BH,MQ=![]() BH,NQ∥CF,NQ=
BH,NQ∥CF,NQ=![]() CF,PM∥CF,PM=
CF,PM∥CF,PM=![]() CF,再根据(2)的结论可得BH=CF,BH⊥CF,然后求出MP=PN=NQ=MQ,从而判定四边形MPNQ是菱形,再根据BH⊥CF求出PN⊥NQ,根据有一个角是直角的菱形是正方形证明.
CF,再根据(2)的结论可得BH=CF,BH⊥CF,然后求出MP=PN=NQ=MQ,从而判定四边形MPNQ是菱形,再根据BH⊥CF求出PN⊥NQ,根据有一个角是直角的菱形是正方形证明.
![]() ∵
∵![]() 和
和![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,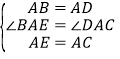 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;

故![]() ,
,![]() 的度数为
的度数为![]() ;
;
![]() 在正方形
在正方形![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,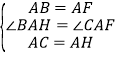 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
设![]() 、
、![]() 相交于点
相交于点![]() ,
,
则![]() ,
,
∴![]() ,
,
故![]() 且
且![]() 与
与![]() 的夹角为
的夹角为![]() ;
;
![]() 四边形
四边形![]() 为正方形.理由如下:
为正方形.理由如下:
∵![]() 、
、![]() 分别是正方形的中心,
分别是正方形的中心,
∴![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∵![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
根据![]() 的结论,
的结论,![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形,
是菱形,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴菱形![]() 是正方形,
是正方形,
故四边形![]() 为正方形.
为正方形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型 | 运费 | |
运往甲地/(元/辆) | 运往乙地/(元/辆) | |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.