题目内容
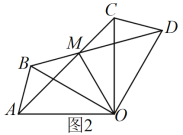
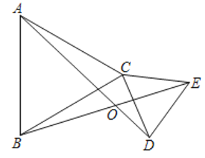
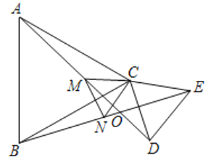
【题目】已知:如图,![]() 、
、![]() 都是等边三角形,
都是等边三角形,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.
的中点.


(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)试判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)见解析;(2)60°;(3)等边三角形,理由见解析
【解析】
(1)根据等边三角形性质得出AC=BC,CD=CE,∠ACB=∠DCE=60°,根据SAS即可证明△ACD≌△BCE.
(2)根据全等求出∠ADC=∠BEC,求出∠ADE+∠BED的值,根据三角形的内角和定理求出即可.
(3)求出AM=BN,根据SAS证△ACM≌△BCN,推出CM=CN,求出∠NCM=60°即可.
(1)∵△ABC、△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
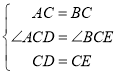 ,
,
∴△ACD≌△BCE(SAS),
(2)∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∵△DCE是等边三角形,
∴∠CED=∠CDE=60°,
∴∠ADE+∠BED
=∠ADC+∠CDE+∠BED
=∠ADC+60°+∠BED
=∠CED+60°
=60°+60°
=120°,
∴∠DOE=180°-(∠ADE+∠BED)=60°;
(3)∵△ACD≌△BCE,
∴∠CAD=∠CBE,AD=BE,AC=BC,

又∵点M、N分别是线段AD、BE的中点,
∴AM=![]() AD,BN=
AD,BN=![]() BE,
BE,
∴AM=BN,
在△ACM和△BCN中,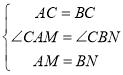 ,
,
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
又∠ACB=60°,
∴∠ACM+∠MCB=60°,
∴∠BCN+∠MCB=60°,
∴∠MCN=60°,
∴△MNC是等边三角形.

 名校课堂系列答案
名校课堂系列答案【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式.(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?