Question

【题目】如图：点P是四边形ABCD外接圆⊙O上的任意一点，且不与四边形顶点重合，若AD是⊙O的直径，AB=BC=CD,连接PA，PB，PC，若PA= ,求点A到PB和PC的距离之和AE＋AF是多少？

Answer 1

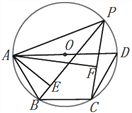
【答案】

【解析】试题分析：

如图，连接BO、CO，由已知条件易证∠AOB=∠BOC=∠COD=60°，从而可得∠APE=∠BPC=30°，∠APF=60°，结合AE⊥BP于点E，AF⊥PC于点F，在Rt△APE和Rt△AOF中，利用30°的锐角所对直角边是斜边的一半，和勾股定理可求得AE和AF的长，然后相加即可得到答案.

试题解析：

连接BO、CO,

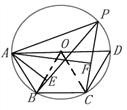
∵AD是⊙O的直径，AB=BC=CD,

∴,

∴∠AOB =∠COB =∠COD= 60°

∴∠APB =∠CPB =30°

∴∠CPA =∠APB +∠CPB =60°

∴∠PAF =30°

∵AE⊥PB，AF⊥PC

∴AE= ，PF= ，

∴AF=，

∴AE＋AF = .