题目内容
【题目】已知抛物线C1：y=x2+2x﹣3与x轴交于点A，B（点A在点B左侧），与y轴交于点C，抛物线C2：y=ax2+bx+c经过点B，与x轴的另一个交点为E（﹣4，0），与y轴交于点D（0，2）．
（1）求抛物线C2的解析式；
（2）设点P为线段AB上一动点（点P不与点A，B重合），过点P作x轴的垂线交抛物线C1于点M，交抛物线C2于点N．
①当四边形AMBN的面积最大时，求点P的坐标；
②当CM=DN≠0时，求点P的坐标．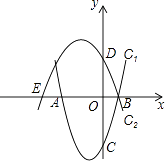
【答案】
（1）
解：在y=x2+2x﹣3中，令y=0可得0=x2+2x﹣3，解得x=﹣3或x=1，令x=0可得y=﹣3，
∴A（﹣3，0），B（1，0），C（0，﹣3），
设抛物线C2的解析式为y=ax2+bx+c，
把B、D、E三点坐标代入可得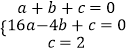 
，解得 
，
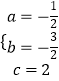∴抛物线C2的解析式为y=﹣ 
x2﹣ 
x+2
（2）
解：设P（x，0）（﹣3＜x＜1），则M（x，x2+2x﹣3），N（x，﹣ x2﹣ x+2），
①∵点P为线段AB上一动点，
∴MN=﹣ x2﹣ x+2﹣（x2+2x﹣3）=﹣ x2﹣ 
x+5，
∴S四边形AMBN= ABMN= ×4（﹣ x2﹣ x+5）=﹣3x2﹣7x+10=﹣3（x+ 
）2+ 
，
∵﹣3＜0，
∴当x=﹣ 时，S四边形AMBN有最大值，
此时P点坐标为（﹣ ，0）；
②分CM和DN平行和不平行两种情况，
当CM与DN不平行时，如图1，作MF⊥CD于F，NG⊥CD于G，
在Rt△MFC和Rt△NGD中
∴Rt△MFC≌Rt△NGD（HL），
∴FC=GD，
∴PM﹣PN=FO﹣OG=OC﹣OD=3﹣2=1，
∴﹣x2﹣2x+3﹣（﹣ x2﹣ x+2）=1，解得x=﹣1或x=0（舍去），
∴P（﹣1，0）；
当CM∥DN时，如图2，
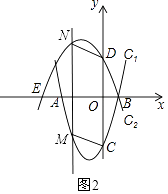
则四边形MNDC为平行四边形，
∴MN=CD=2+3=5，
∴﹣ x2﹣ x+5=5，解得x=0（舍去）或x=﹣ 
，
∴P（﹣ ，0）；
综上可知P点坐标为（﹣1，0）或（﹣ ，0）
【解析】（1）可先求得A、B、C的坐标，利用待定系数法可求得抛物线C2的解析式；（2）可设P（x，0），①则可表示出M、N的坐标，可表示出MN的长，从而可用x表示出四边形AMBN的面积，利用二次函数的性质可求得当其取最大值时x的值，可求得P点坐标；②分CM和DN平行和不平行两种情况，分别构造全等三角形可得到关于x的方程，从而可求得P点坐标．
【考点精析】本题主要考查了二次函数的性质和二次函数的最值的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a才能正确解答此题．
