题目内容
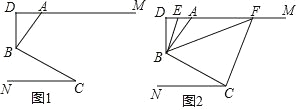
【题目】如图,已知四边形ABCD中,∠B+∠D=180°,AC平分∠BAD,CE⊥AD,E为垂足.求证:AB+AD=2AE.

【答案】证明见解析.
【解析】
过点C作CH⊥AB,交AB的延长线于点H.利用角平分线性质得CH=CE,∠HCA=∠ECA,证△ACH≌△ACE(AAS),得AH=AE.∠HBC=∠D.再证△BHC≌△DEC(AAS),得HB=DE,
所以AB+AD=AB+AE+DE=AB+AE+HB=AH+AE=2AE.
证明:如图,过点C作CH⊥AB,交AB的延长线于点H.

∵AC平分∠BAD,CE⊥AD,
∴CH=CE,∠HCA=∠ECA(等角的余角相等).
在△ACH和△ACE中,
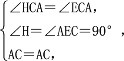
∴△ACH≌△ACE(AAS),
∴AH=AE.
又∵∠ABC+∠HBC=180°,
∠ABC+∠D=180°,
∴∠HBC=∠D.
在△BHC和△DEC中,
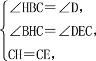
∴△BHC≌△DEC(AAS),
∴HB=DE,
∴AB+AD=AB+AE+DE=AB+AE+HB=AH+AE=2AE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
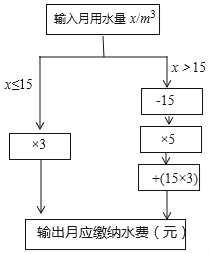
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.