题目内容
【题目】如图,O为直线AB上一点,∠BOC=α.
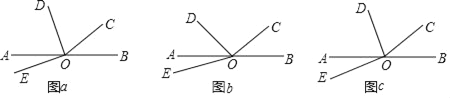
(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;
(2)若∠AOD=![]() ∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
(3)若∠AOD=![]() ∠AOC,∠DOE=
∠AOC,∠DOE=![]() (n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
(n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
【答案】(1)20°;(2)∠AOE=![]() α;(3)∠AOE=
α;(3)∠AOE=![]() .
.
【解析】
(1)利用角平分线的性质得出∠AOD=∠DOC=70°,进而得出∠AOE的度数;
(2)利用设∠AOD=x,则∠DOC=2x,∠BOC=180-3x=α,得出x的值,进而用α表示∠AOE的度数;
(3)利用(2)中作法,得出x与α的关系,进而得出答案.
(1)∵∠BOC=40°,OD平分∠AOC,
∴∠AOD=∠DOC=70°,
∵∠DOE=90°,则∠AOE=90°﹣70°=20°;
故答案为:20°;
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180﹣3x=α,
解得:x= ![]() ,
,
∴∠AOE=60﹣x=60﹣![]() =
= ![]() ;
;
(3)设∠AOD=x,则∠DOC=(n﹣1)x,∠BOC=180﹣nx=α,
解得:x=![]() ,
,
∴∠AOE= ![]() ﹣
﹣![]() =
= ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目