题目内容
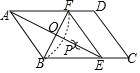
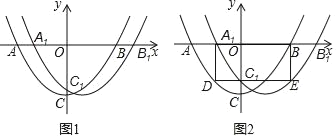
【题目】如图所示,二次函数y=ax2+bx+2的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
(1)请求出二次函数的解析式;
(2)若点M(m,n)在抛物线的对称轴上,且AM平分∠OAC,求n的值.
(3)若P是线段AB上的一个动点(不与A、B重合),过P作PQ∥AC,与AB上方的抛物线交于点Q,与x轴交于点H,试问:是否存在这样的点Q,使PH=2QH?若存在,请直接出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)2
x+2;(2)2![]() ﹣6;(3)存在,点Q(﹣
﹣6;(3)存在,点Q(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
(1)将点A、B的坐标代入函数表达式,即可求解;
(2)如图,过点A作∠A的角平分线交y轴于点M,则由勾股定理得:(2﹣x)2=x2+(2![]() ﹣4)2,解得:x=4
﹣4)2,解得:x=4![]() ﹣8,即可求解;
﹣8,即可求解;
(3)确定直线AB、直线PQ的表达式,联立求得点Q(2﹣2![]() ,﹣1﹣c+
,﹣1﹣c+![]() ),由PH=2QH,则P、Q的纵坐标之比也为2,即可求解.
),由PH=2QH,则P、Q的纵坐标之比也为2,即可求解.
解:(1)将点A、B的坐标代入函数表达式得:![]() ,解得:
,解得: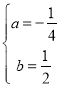 ,
,
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)如图,过点A作∠A的角平分线交y轴于点M,交二次函数对称轴于点G,
过点M作MN⊥AC于点N,二次函数对称轴交AM、x轴于点G、H,
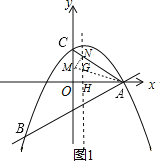
设:OM=x=MN,则AM=OA=4,
AC=2![]() ,OC=2,CM=2﹣x,CN=CA﹣AN=2
,OC=2,CM=2﹣x,CN=CA﹣AN=2![]() ﹣4,
﹣4,
则由勾股定理得:(2﹣x)2=x2+(2![]() ﹣4)2,解得:x=4
﹣4)2,解得:x=4![]() ﹣8,
﹣8,
∴GH∥OM,则![]() ,即:
,即:![]() ,
,
则n=GH=![]() x=2
x=2![]() ﹣6;
﹣6;
(3)存在,理由:
如图:
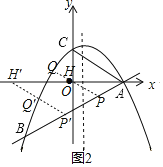
将点B、A的坐标代入一次函数表达式并解得:
直线AB的表达式为:y=![]() x﹣2①,
x﹣2①,
同理直线AC的表达式为:y=﹣![]() x+2,
x+2,
∵PQ∥AC,则设直线PQ的表达式为:y=﹣![]() x﹣c(c>0)②,
x﹣c(c>0)②,
联立①②并解得:x=2±2![]() (舍去正值),
(舍去正值),
故点Q(2﹣2![]() ,﹣1﹣c+
,﹣1﹣c+![]() ),
),
∵PH=2QH,
∴P、Q的纵坐标之比也为2,
即﹣![]() c﹣1=±2(﹣1﹣c+
c﹣1=±2(﹣1﹣c+![]() ),
),
解得:c=![]() 或
或![]() ,
,
故点Q(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).

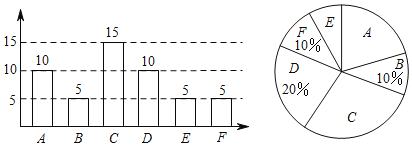
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
【题目】某校为了解九年级学生每天参加体育锻炼额时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):
30 60 70 10 30 115 70 60 75 90 15 70 40 75 105 80 60 30 70 45
对以上数据进行整理分析,得到下列表一和表二:
表一
时间t(单位:分钟) |
|
|
|
|
人数 | 2 | a | 10 | b |
表二
平均数 | 中位数 | 众数 |
60 | c | d |
根据以上提供信息,解答下列问题:
(1)填空
①a= b=
②c= d=
(2)如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数。