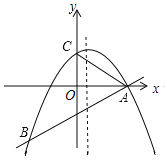题目内容
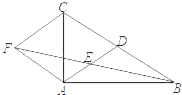
【题目】如图1,将抛物线P1:y1=![]() x2﹣3右移m个单位长度得到新抛物线P2:y2=a(x+h)2+k,抛物线P1与x轴交于A、B两点,与y轴交于点C,抛物线P2与x轴交于A1,B1两点,与y轴交于点C1.
x2﹣3右移m个单位长度得到新抛物线P2:y2=a(x+h)2+k,抛物线P1与x轴交于A、B两点,与y轴交于点C,抛物线P2与x轴交于A1,B1两点,与y轴交于点C1.
(1)当m=1时,a= ,h= ,k= ;
(2)在(1)的条件下,当y1<y2<0时,求x的取值范围;
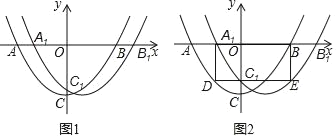
(3)如图2,过点C1作y轴的垂线,分别交抛物线P1,P2于D、E两点,当四边形A1DEB是矩形时,求m的值.
【答案】(1)![]() ;﹣1,﹣3(2)﹣2<x<
;﹣1,﹣3(2)﹣2<x<![]() (3)
(3)![]()
【解析】
(1)根据平移的坐标特征写出抛物线平移后得到的解析式,与抛物线P2解析式对应即得到a、h、k的值.
(2)把y1<y2<0拆分成两部分:①求y2<0时x的取值范围,先求出抛物线P2与x轴两交点坐标,由图象可知在抛物线中间部分在x轴下方,即对应的x范围;②求y1<y2时x的取值范围,先由两二次函数值相等求得两抛物线交点横坐标,根据图象找出x对应的取值范围;①②部分要同时成立,即求关于x的两个不等式组的公共解.
(3)根据平移后图象上所有点平移的距离相等,都是m,得到AA1=DC1=m,由四边形A1DEB是矩形易证四边形A1DC1O是矩形,即得到OA=AA1+OA1=2m=3.
解:(1)∵抛物线P1:y1=![]() x2﹣3右移m个单位长度得到新抛物线解析式为:y2=
x2﹣3右移m个单位长度得到新抛物线解析式为:y2=![]() (x﹣m)2﹣3
(x﹣m)2﹣3
∴y2=a(x+h)2+k=![]() (x﹣m)2﹣3
(x﹣m)2﹣3
又∵m=1
∴h=﹣m=﹣1
故答案为:![]() ;﹣1,﹣3
;﹣1,﹣3
(2)∵当y2=![]() (x﹣1)2﹣3=0时,
(x﹣1)2﹣3=0时,
解得:x1=﹣2,x2=4
∴由图象可知,当﹣2<x<4时,y2<0
当y1=y2时,![]() x2﹣3=
x2﹣3=![]() (x﹣1)2﹣3
(x﹣1)2﹣3
解得:x=![]() ,
,
∴由图象可知,当x<![]() 时,y1<y2
时,y1<y2
∴当y1<y2<0时,x的取值范围是﹣2<x<![]()
(3)当y1=![]() x2﹣3=0时,解得:x=±3
x2﹣3=0时,解得:x=±3
∴A(﹣3,0),OA=3
根据平移性质得:AA1=DC1=m
∵四边形A1DEB是矩形
∴∠A1DE=∠DA1B=90°
∴四边形A1DC1O是矩形
∴OA1=DC1=m
∴OA=AA1+OA1=2m=3
∴m=![]()