题目内容
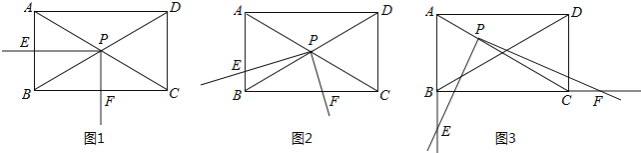
【题目】如图,∠A=∠B=30°,P为AB中点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.
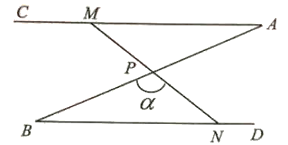
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。
【答案】(1)见解析;(2)30°;(3)![]()
【解析】
(1)由P为AB的中点,可得PA=PB,再由已知中∠A=∠B=30°,对顶角∠APM=∠BPN,根据ASA即可判定△APM≌△BPN;
(2)由(1)中结论可知PM=PN,即MN=2PN,由已知MN=2BN,可得BN=PN,根据等边对等角,即α=∠B=30°;
(3)当α=60°时,由∠B=30°,可知MN⊥BD,此时BP的中点为△BPN的外心,当α=90°时,由∠B=30°,此时BN的中点为△BPN的外心,根据三角形中位线定理可得△BPN的外心运动路线的长度为PN的一半,即为![]() .
.
(1)证明:∵P是AB的中点,∴PA=PB , 在△APM和△BPN中, 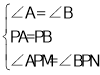
∴△APM≌△BPN(ASA)
(2)解:由(1)得:△APM≌△BPN , ∴PM=PN , ∴MN=2PN , ∵MN=2BN , ∴BN=PN , ∴α=∠B=30°
(3)解: ![]()

练习册系列答案
相关题目