��Ŀ����
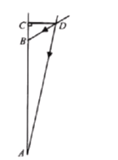
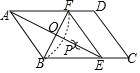
����Ŀ����ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() BFΪ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
BFΪ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��1��AB�� ��AF��ѡ�������������١���������������������AE�� ����BAD��ƽ���ߣ���ѡ��������������������
��2���ڣ�1���������£���֤���ı���ABEF�����Σ�
��3��AE��BF�ཻ�ڵ�O�����ı���ABEF���ܳ�Ϊ40��BF��10����AE�ij�Ϊ�� ������ABC���� ������
���𰸡���1�������ǣ���2������������3��![]() .
.
��������
��1�����ݽ�ƽ�ֵ����ʺͳ߹���ͼԭ�����ɵõ��𰸣�
��2����֤����AEB�ա�AEF���Ƴ���EAB=��EAF����AD��BC���Ƴ���EAF=��AEB=��EAB���õ�BE=AB=AF���ɴ˼���֤����
��3���������ε���������֤����AOB�Ǻ���30����ֱ�������Σ��ɴ˼��ɽ�����⣮
��1���⣺AB��AF��AEƽ�֡�BAD��ƽ���ߣ�
�ʴ�Ϊ�����ǣ�
��2��֤������AEƽ�֡�BAF��
���BAE����FAE��
��AF��BE��
���BAE����BEA��
��AB��EB��
��AF��AB��
��AF��BE��AF��BE��
���ı���ABEFΪƽ���ı��Σ�
��AB��AF��
���ı���ABEF�����Σ�
��3���⣺���ı���ABEF�����Σ�
���ı���ABEF���ܳ�Ϊ40��
��AB��10��OA��OE��OB��OF��5��AE��BF��
���ABFΪ�ȱ������Σ�
���BAF��60����
���ABC��120����
��OA��![]() OB��5
OB��5![]() ��
��
��AE��2OA��10![]() ��
��
�ʴ�Ϊ10![]() ��120��
��120��