Question

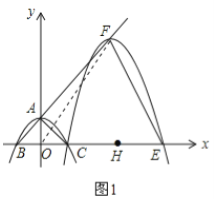
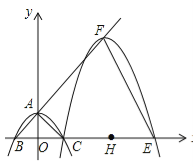
【题目】如图，抛物线（）与y轴交于点A，与x轴交于B，C两点（点C在x轴正半轴上），△ABC为等腰直角三角形，且面积为4，现将抛物线沿BA方向平移，平移后的抛物线过点C时，与x轴的另一点为E，其顶点为F，对称轴与x轴的交点为H．

（1）求a、c的值及抛物线的解析式．

（2）连接OF，试判断△OEF是否为等腰三角形，并说明理由．

Answer 1

【答案】（1）a=，c=2；（2）△OEF是等腰三角形.

【解析】

试题分析：（1）由A（0，c），得到OA=c，再由等腰直角三角形的性质得OA=OB=OC=c，由三角形面积公式解得，解得c=2，把C（2，0）代入可求出a的值；

（2）如图1，先利用待定系数法求出直线AB的解析式为，设F（t，t+2），利用抛物线平移的规律可设平移后的抛物线解析式为，再把C（2，0）代入解得t=6，则平移后的抛物线解析式为，所以F（6，8），利用勾股定理得出OF=10，由抛物线与x轴的交点确定E（10，0），则OE=OF=10，于是可判断△OEF为等腰三角形；

试题解析：解：（1）∵抛物线（）与y轴交于点A，

∴A（0，c），则OA=c，

∵△ABC为等腰直角三角形，

∴OA=OB=OC=c，

∴c2c=4，解得c=2，

∴C（2，0），

把C（2，0）代入得4a+2=0，解得a=；

抛物线的解析式是：.

（2）△OEF是等腰三角形．理由如下：如图1，

设直线AB的解析式为，

把A（0，2）、B（﹣2，0）代入得，解得：，

则直线AB的解析式为，设F（t，t+2），

∵抛物线沿BA方向平移，平移后的抛物线过点C时，顶点为F，

∴平移后的抛物线解析式为，

把C（2，0）代入得，解得t=6，

∴平移后的抛物线解析式为，

∴F（6，），

∴OF==10，

令y=0时，，解得，，

∴OE=10，

∴OE=OF，

∴△OEF为等腰三角形；