题目内容
【题目】已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.AD与BE平行吗?为什么?
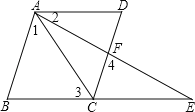
解:AD∥BE,理由如下:
∵AB∥CD(已知)
∴∠4= ( )
∵∠3=∠4(已知)
∴∠3= ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即 =
∴∠3= ( )
∴AD∥BE( )
【答案】见解析
【解析】
试题分析:根据已知条件和解题思路,利用平行线的性质和判定填空.
解:AD∥BE,理由如下:
∵AB∥CD(已知),
∴∠4=∠BAE(两直线平行,同位角相等);
∵∠3=∠4(已知),
∴∠3=∠BAE(等量代换);
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等量代换),
即∠BAF=∠DAC,
∴∠3=∠DAC(等量代换),
∴AD∥BE(内错角相等,两直线平行).

练习册系列答案
相关题目
【题目】某公司欲招聘一名工作人员,对甲、乙两位应聘者进行了笔试和面试,他们的成绩如下表所示:
候选人 | 测试成绩(百分制) | |
笔试 | 面试 | |
甲 | 95 | 85 |
乙 | 83 | 95 |
根据需要,笔试与面试的成绩按4:6的比例确定个人成绩(成绩高者被录用),那么谁将被录用?