题目内容
王聪同学动手剪了若干张如图所示的正方形与长方形纸片．
（1）拼成如图所示的正方形，根据四个小纸片的面积和等于大纸片（正方形）的面积，有a2+2ab+b2=（a+b）2，验证了完全平方公式（分解因式）；
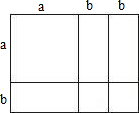
（2）拼成如图所示的矩形，由面积可得a2+3ab+2b2=（a+2b）（a+b），多项式a2+3ab+2b2分解因式的结果是表示矩形长、宽两个整式（a+2b）与（a+b）的积．
问题：
①动手操作一番，利用拼图分解因式a2+5ab+6b2=______．
②猜想面积为2a2+5ab+2b2的矩形的长、宽可能分别为______．
（1）拼成如图所示的正方形，根据四个小纸片的面积和等于大纸片（正方形）的面积，有a2+2ab+b2=（a+b）2，验证了完全平方公式（分解因式）；
（2）拼成如图所示的矩形，由面积可得a2+3ab+2b2=（a+2b）（a+b），多项式a2+3ab+2b2分解因式的结果是表示矩形长、宽两个整式（a+2b）与（a+b）的积．
问题：
①动手操作一番，利用拼图分解因式a2+5ab+6b2=______．
②猜想面积为2a2+5ab+2b2的矩形的长、宽可能分别为______．
①a2+5ab+6b2=（a+2b）（a+3b）；
②2a2+5ab+2b2=（a+2b）（2a+b），
∴矩形的长、宽可能分别为a+2b，2a+b．
②2a2+5ab+2b2=（a+2b）（2a+b），
∴矩形的长、宽可能分别为a+2b，2a+b．
练习册系列答案
相关题目