题目内容
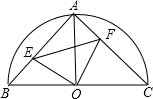
如图,在半径为r的半圆⊙O中,半径OA⊥直径BC,点E、F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
(1)求证:S四边形AEOF=
r2;
(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式及自变量x的范围;
(3)当S△OEF=
S△ABC时,求点E、F分别在AB、AC上的位置及EF的长.
(1)求证:S四边形AEOF=
| 1 |
| 2 |
(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式及自变量x的范围;
(3)当S△OEF=
| 5 |
| 18 |

(1)证明:∵OA=OC,AE=CF,∠EAO=∠C=45°
∴△AOE≌△COF,
∴四边形AEOF的面积=△AOC的面积=
r2.
(2)∵S△OEF=S四边形AEOF-S△AEF=
r2-
(
r-x)•x=
x2-
rx+
r2,
∴y=
x2-
rx+
r2(0<x<
r)
(3)当S△OEF=
S△ABC时,y=
r2
∴
x2-
rx+
r2=
r2
∴x1=
r,x2=
r,
∴
=
,
=
或
=
,
=
即AE=
AB,AF=
AC或AE=
AB,AF=
AC.
∴EF=
r.
∴△AOE≌△COF,
∴四边形AEOF的面积=△AOC的面积=
| 1 |
| 2 |
(2)∵S△OEF=S四边形AEOF-S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴y=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
(3)当S△OEF=
| 5 |
| 18 |
| 5 |
| 18 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 18 |
∴x1=
| ||
| 3 |
2
| ||
| 3 |
∴
| AE |
| AB |
| 1 |
| 3 |
| AF |
| AC |
| 2 |
| 3 |
| AE |
| AB |
| 2 |
| 3 |
| AF |
| AC |
| 1 |
| 3 |
即AE=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
∴EF=
| ||
| 3 |

练习册系列答案
相关题目
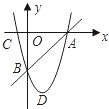
 A(m,0)、B(0,n).
A(m,0)、B(0,n).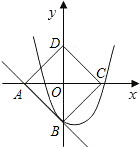 y=x2+bx+c经过点B且与直线AB只有一个公共点.
y=x2+bx+c经过点B且与直线AB只有一个公共点.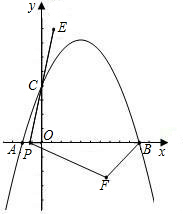 ,(0,2).
,(0,2).