Question

如图，以边长为

2

的正方形ABCD的对角线所在直线建立平面直角坐标系，抛物线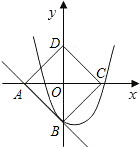y=x²+bx+c经过点B且与直线AB只有一个公共点．
（1）求直线AB的解析式；
（2）求抛物线y=x²+bx+c的解析式；
（3）若点P为（2）中抛物线上一点，过点P作PM⊥x轴于点M，问是否存在这样的点P，使△PMC∽△ADC？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

（1）设直线AB的解析式为：y=kx+b，
由已知可得A（-1，0），B（0，-1）则

-k+b=0 b=-1

∴

k=-1 b=-1

∴直线AB的解析式为：y=-x-1

（2）把B（0，-1）代入抛物线y=x²+bx+c中得c=-1，联立

y=-x-1 y=x2+bx-1

得x²+（b+1）x=0，
当△=0时，解得b=-1，
∴抛物线解析式为：y=x²-x-1

（3）存在这样的点P，使△PMC∽△ADC，
∵△ADC为等腰直角三角形，则△PMC为等腰直角三角形，
即CM=PM=m，
又OC=1，根据图象P点坐标可设为（1+m，m），（1-m，m），（1-m，-m），
代入抛物线解析式y=x²-x-1中，
解方程：（1+m）²-（1+m）-1=m，
（1-m）²-（1-m）-1=m，
（1-m）²-（1-m）-1=-m；
解得m=-1，1，1±

2

，
∴P点的坐标为（0，-1），（2，1），（

2

，1-

2

），（-

2

，1+

2

）．