题目内容
如图,抛物线y=-
x2+
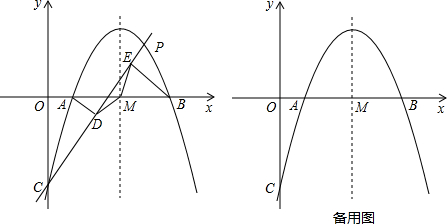
x-4与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
(1)求点A,B的坐标(直接写出结果),并证明△MDE是等腰三角形;
(2)△MDE能否为等腰直角三角形?若能,求此时点P的坐标;若不能,说明理由;
(3)若将“P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上)”改为“P是抛物线在x轴下方的一个动点”,其他条件不变,△MDE能否为等腰直角三角形?若能,求此时点P的坐标(直接写出结果);若不能,说明理由.
| 4 |
| 5 |
| 24 |
| 5 |
(1)求点A,B的坐标(直接写出结果),并证明△MDE是等腰三角形;
(2)△MDE能否为等腰直角三角形?若能,求此时点P的坐标;若不能,说明理由;
(3)若将“P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上)”改为“P是抛物线在x轴下方的一个动点”,其他条件不变,△MDE能否为等腰直角三角形?若能,求此时点P的坐标(直接写出结果);若不能,说明理由.

(1)抛物线解析式为y=-
x2+
x-4,令y=0,
即-
x2+
x-4=0,解得x=1或x=5,∴A(1,0),B(5,0).
如答图1所示,分别延长AD与EM,交于点F.
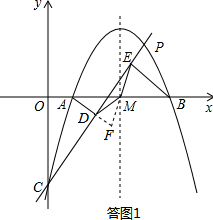
∵AD⊥PC,BE⊥PC,∴AD∥BE,∴∠MAF=∠MBE.
在△AMF与△BME中,
,
∴△AMF≌△BME(ASA),
∴ME=MF,即点M为Rt△EDF斜边EF的中点,
∴MD=ME,即△MDE是等腰三角形.
(2)答:能.
抛物线解析式为y=-
x2+
x-4=-
(x-3)2+
,
∴对称轴是直线x=3,M(3,0);
令x=0,得y=-4,∴C(0,-4).
△MDE为等腰直角三角形,有3种可能的情形:
①若DE⊥EM,
由DE⊥BE,可知点E、M、B在一条直线上,
而点B、M在x轴上,因此点E必然在x轴上,
由DE⊥BE,可知点E只能与点O重合,即直线PC与y轴重合,
不符合题意,故此种情况不存在;
②若DE⊥DM,与①同理可知,此种情况不存在;
③若EM⊥DM,如答图2所示:

设直线PC与对称轴交于点N,
∵EM⊥DM,MN⊥AM,∴∠EMN=∠DMA.
在△ADM与△NEM中,
∴△ADM≌△NEM(ASA),
∴MN=MA.
抛物线解析式为y=-
x2+
x-4=-
(x-3)2+
,故对称轴是直线x=3,
∴M(3,0),MN=MA=2,
∴N(3,2).
设直线PC解析式为y=kx+b,∵点N(3,2),C(0,-4)在直线上,
∴
,解得k=2,b=-4,∴y=2x-4.
将y=2x-4代入抛物线解析式得:2x-4=-
x2+
x-4,
解得:x=0或x=
,
当x=0时,交点为点C;当x=
时,y=2x-4=3.
∴P(
,3).
综上所述,△MDE能成为等腰直角三角形,此时点P坐标为(
,3).
(3)答:能.
如答题3所示,设对称轴与直线PC交于点N.
与(2)同理,可知若△MDE为等腰直角三角形,直角顶点只能是点M.
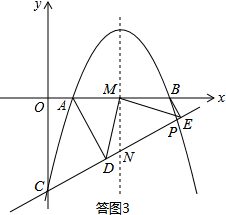
∵MD⊥ME,MA⊥MN,∴∠DMN=∠EMB.
在△DMN与△EMB中,
,
∴△DMN≌△EMB(ASA),
∴MN=MB.
∴N(3,-2).
设直线PC解析式为y=kx+b,∵点N(3,-2),C(0,-4)在抛物线上,
∴
,解得k=
,b=-4,∴y=
x-4.
将y=
x-4代入抛物线解析式得:
x-4=-
x2+
x-4,
解得:x=0或x=
,
当x=0时,交点为点C;当x=
时,y=
x-4=-
.
∴P(
,-
).
综上所述,△MDE能成为等腰直角三角形,此时点P坐标为(
,-
).
| 4 |
| 5 |
| 24 |
| 5 |
即-
| 4 |
| 5 |
| 24 |
| 5 |
如答图1所示,分别延长AD与EM,交于点F.

∵AD⊥PC,BE⊥PC,∴AD∥BE,∴∠MAF=∠MBE.
在△AMF与△BME中,
|
∴△AMF≌△BME(ASA),
∴ME=MF,即点M为Rt△EDF斜边EF的中点,
∴MD=ME,即△MDE是等腰三角形.
(2)答:能.
抛物线解析式为y=-
| 4 |
| 5 |
| 24 |
| 5 |
| 4 |
| 5 |
| 16 |
| 5 |
∴对称轴是直线x=3,M(3,0);
令x=0,得y=-4,∴C(0,-4).
△MDE为等腰直角三角形,有3种可能的情形:
①若DE⊥EM,
由DE⊥BE,可知点E、M、B在一条直线上,
而点B、M在x轴上,因此点E必然在x轴上,
由DE⊥BE,可知点E只能与点O重合,即直线PC与y轴重合,
不符合题意,故此种情况不存在;
②若DE⊥DM,与①同理可知,此种情况不存在;
③若EM⊥DM,如答图2所示:

设直线PC与对称轴交于点N,
∵EM⊥DM,MN⊥AM,∴∠EMN=∠DMA.
在△ADM与△NEM中,
|
∴△ADM≌△NEM(ASA),
∴MN=MA.
抛物线解析式为y=-
| 4 |
| 5 |
| 24 |
| 5 |
| 4 |
| 5 |
| 16 |
| 5 |
∴M(3,0),MN=MA=2,
∴N(3,2).
设直线PC解析式为y=kx+b,∵点N(3,2),C(0,-4)在直线上,
∴
|
将y=2x-4代入抛物线解析式得:2x-4=-
| 4 |
| 5 |
| 24 |
| 5 |
解得:x=0或x=
| 7 |
| 2 |
当x=0时,交点为点C;当x=
| 7 |
| 2 |
∴P(
| 7 |
| 2 |
综上所述,△MDE能成为等腰直角三角形,此时点P坐标为(
| 7 |
| 2 |
(3)答:能.
如答题3所示,设对称轴与直线PC交于点N.
与(2)同理,可知若△MDE为等腰直角三角形,直角顶点只能是点M.

∵MD⊥ME,MA⊥MN,∴∠DMN=∠EMB.
在△DMN与△EMB中,
|
∴△DMN≌△EMB(ASA),
∴MN=MB.
∴N(3,-2).
设直线PC解析式为y=kx+b,∵点N(3,-2),C(0,-4)在抛物线上,
∴
|
| 2 |
| 3 |
| 2 |
| 3 |
将y=
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 5 |
| 24 |
| 5 |
解得:x=0或x=
| 31 |
| 6 |
当x=0时,交点为点C;当x=
| 31 |
| 6 |
| 2 |
| 3 |
| 5 |
| 9 |
∴P(
| 31 |
| 6 |
| 5 |
| 9 |
综上所述,△MDE能成为等腰直角三角形,此时点P坐标为(
| 31 |
| 6 |
| 5 |
| 9 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
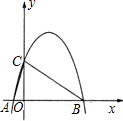 OC相似?若存在,求出n的值,并画出相应的示意图;若不存在,请说明理由.
OC相似?若存在,求出n的值,并画出相应的示意图;若不存在,请说明理由. 边上)的一个动点,点C在y轴上,抛物线y=ax2+bx+1以P为顶点.
边上)的一个动点,点C在y轴上,抛物线y=ax2+bx+1以P为顶点.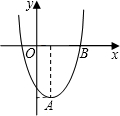
 只鳗鱼上升到第6年2万只.乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.
只鳗鱼上升到第6年2万只.乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个. 1,0),顶点为B.
1,0),顶点为B.