题目内容
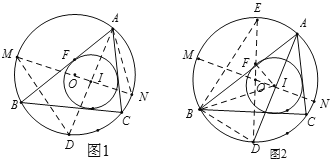
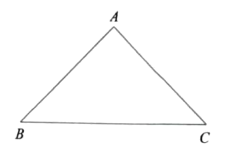
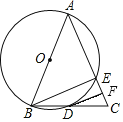
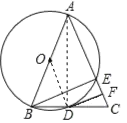
【题目】如图,AB是⊙O的直径,AB=AC,AC交⊙O于点E,BC交⊙O于点D,F是CE的中点,连接DF.则下列结论错误的是
A.∠A=∠ABEB.![]()
C.BD=DCD.DF是⊙O的切线
【答案】A
【解析】
首先由AB是⊙O的直径,得出AD⊥BC,推出BD=DC,再由OA=OB,推出OD是△ABC的中位线,得DF⊥OD,即DF是⊙O的切线,最后由假设推出不正确.
解:连接OD,AD.
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角),
∴AD⊥BC;
而在△ABC中,AB=AC,
∴AD是边BC上的中线,
∴BD=DC(C选项正确);
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴DB=DC,∠BAD=∠CAD,
∴![]() ,(B选项正确);
,(B选项正确);
∵OA=OB,
∴OD是△ABC的中位线,
即:OD∥AC,
∵DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线(D选项正确);
只有当△ABE是等腰直角三角形时,∠A=∠ABE=45°,
故A选项错误,
故选A.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目