Question

【题目】四边形是正方形，将线段绕点逆时针旋转，得到线段，连接，过点作交的延长线于，连接．

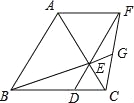
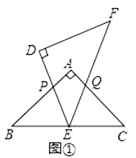
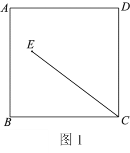
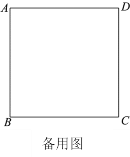
（1）依题意补全图1；

（2）直接写出的度数；

（3）连接，用等式表示线段与的数量关系，并证明．

Answer 1

【答案】（1）见解析；（2）；（3），理由见解析

【解析】

（1）按照题中的表述画出图形即可；
（2）由题意可知，CD=CE=CB，∠ECD=2α，∠ABC=∠BCD=∠CDA=∠DAB=90°，根据题中角度关系推理即可；
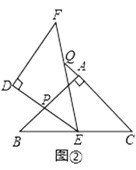
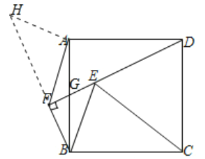
（3）作AH⊥AF，交BF的延长线于点H，先通过条件证明△HAB≌△FAD，可得HB=FD，AH=AF，HF=DE，∠H=45°，从而知道HF与AF的数量关系，即可得线段AF与DE的数量关系．

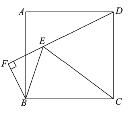
解：（1）补全图形，如图所示．

（2），

设DF与AB交于点G，如图所示：

由题意得，CD=CE=CB，∠ECD=2α，∠ABC=∠BCD=∠CDA=∠DAB=90°，
∴∠EDC=90°-α，∠BCE=90°-2α，
∴∠CBE=45°+α，∠ADF=α，
∴∠ABE=45°-α．
∵BF⊥DE，
∴∠BFD=90°．
∵∠AGD=∠FGB，
∴∠FBG=α
∴∠FBE=∠FEB=45°；

（3）．

证明：如图，作，交的延长线于点，设与交于点，

根据题意可知，．

．

．

．

，

．

，

．

．

．

，

．

．

．

．

．

．