��Ŀ����
����Ŀ���Ķ����²��ϣ�����Ҫ�������Ӧ������
����������ŷ��(Leonhard Euler)����ʿ��ѧ�ң�����ѧ�Ͼ�������������������������Ҫ��������ʽ�Ͷ�����������ŷ�����ֵ�һ������������ABC�У�R��r�ֱ�Ϊ���Բ������Բ�İ뾶��O��I�ֱ�Ϊ�����ĺ����ģ���![]() .
.
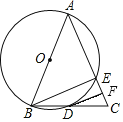
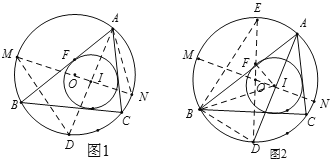
��ͼ1����O�͡�I�ֱ��ǡ�ABC�����Բ������Բ����I��AB���з��ڵ�F�����O�İ뾶ΪR����I�İ뾶Ϊr������O�����������ߴ�ֱƽ���ߵĽ��㣩������I��������������ƽ���ߵĽ��㣩֮��ľ���OI��d������d2��R2��2Rr��
�����Ǹö�����֤�����̣����֣���
�ӳ�AI����O�ڵ�D������I����O��ֱ��MN������DM��AN.
�ߡ�D=��N����DMI=��NAI(ͬ�����Ե�Բ�ܽ����)��
���MDI�ס�ANI��
��![]() ��
��
��![]() �٣�
�٣�
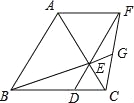
��ͼ2����ͼ1(��ȥMD��AN)�Ļ���������O��ֱ��DE������BE��BD��BI��IF��
��DE����O��ֱ�������DBE=90����
�ߡ�I��AB�����ڵ�F�����AFI=90����
���DBE=��IFA��
�ߡ�BAD=��E(ͬ������Բ�ܽ����)��
���AIF�ס�EDB��
��![]() ����
����![]() �ڣ�
�ڣ�
����(1)�۲췢�֣�![]() ��
��![]() (�ú�R��d�Ĵ���ʽ��ʾ)��
(�ú�R��d�Ĵ���ʽ��ʾ)��
(2)���ж�BD��ID��������ϵ����˵�����ɣ�
(3)��۲�ʽ�Ӣٺ�ʽ�Ӣڣ�����������(1)��(2)�Ľ��ۣ����������֤��˼·����ɸö���֤����ʣ�ಿ�֣�
(4)Ӧ�ã�����ABC�����Բ�İ뾶Ϊ5cm������Բ�İ뾶Ϊ2cm������ABC������������֮��ľ���Ϊ cm.

���𰸡�(1)R-d��(2)BD=ID�����ɼ�������(3)��������(4)![]() .
.
��������
(1)ֱ�ӹ۲�ɵã�
(2)�����������ĵ����ʿɵá�BAD=��CAD����CBI=��ABI����Բ�ܽǶ����ɵá�DBC=��CAD���ٸ�����������ǵ����ʼ�����á�BID=��DBI���̶���֤��BD=ID��
(3)Ӧ��(1)(2)���ۼ��ɣ�
(4)ֱ�Ӵ�����۽��м��㼴�ɣ�
(1)��O��I��N���㹲�ߣ�
��OI+IN��ON��
��IN��ON��OI��R��d��
�ʴ�Ϊ��R��d��
(2)BD=ID���������£�
����I����ABC�����ģ�
���BAD=��CAD����CBI=��ABI��
�ߡ�DBC=��CAD����BID=��BAD+��ABI����DBI=��DBC+��CBI��
���BID=��DBI��
��BD=ID��
(3)��(2)֪��BD=ID��
��![]() ��
��![]() ��
��
��DE��IF=IM��IN��
��![]() ��
��
��![]()
��![]() ��
��
(4)��(3)֪��![]() ��
��
��R=5��r=2����ã�![]() ��
��
��d>0��
��![]() ��
��
�ʴ�Ϊ��![]() .
.

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�