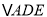题目内容
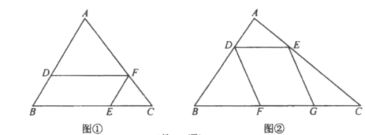
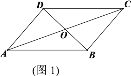
【题目】我们把有两边对应相等，且夹角互补(不相等)的两个三角形叫做“互补三角形”，如图1，□ABCD中，△AOB和△BOC是“互补三角形”.
(1)写出图1中另外一组“互补三角形”_______；
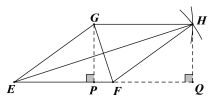
(2)在图2中，用尺规作出一个△EFH，使得△EFH和△EFG为“互补三角形”，且△EFH和△EFG在EF同侧，并证明这一组“互补三角形”的面积相等.
【答案】(1)答案不唯一，△AOD和△AOB，△ABD和△ABC；(2)如图所示，见解析.
【解析】
（1）根据“互补三角形”的定义解答.
（2）在G点同侧作GH=EF.FH=EG，则四边形EFHG是平行四边形，根据“互补三角形”的定义，△EFH和△EFG为“互补三角形”， 且△EFH和△EFG是同底等高的，即面积相等.
(1)答案不唯一，如：△AOD和△AOB，△ABD和△ABC
(2)如图所示，△EFH为所求作的三角形，
∵GH=EF，FH=EG，
∴四边形EFHG是平行四边形，
∴GH∥EF，GP＝HQ，△EFH和△EFG同底等高，三角形面积相等.
练习册系列答案
通城学典默写能手系列答案
相关题目
【题目】已知函数
，请根据已学知识探究该函数的图象和性质过程如下：
（1）该函数自变量的取值范围为；
（2）下表列出y与x的几组对应值，请在平面直角坐标系中描出下列各点，并画出函数图象；
x | … |
|
| -1 |
| 2 |
|
| … |
y | … | 3 | 2 | 1 |
|
|
|
| … |
（3）结合所画函数图象，解决下列问题：
①写出该函数图象的一条性质：；
②横、纵坐标均为整数的点称为整点，若直线y= -x+b的图象与该图象相交形成的封闭图形（包含边界）内刚好有6个整点，则b的取值范围为．
