题目内容
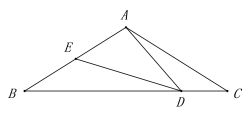
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,边
的等边三角形,边![]() 在射线
在射线![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将
出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将![]() 绕点C逆时针方向旋转60°得到
绕点C逆时针方向旋转60°得到![]() ,连接DE.
,连接DE.
(1)如图1,求证:![]() 是等边三角形;
是等边三角形;
(2)如图2,当6<t<10时,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
(3)当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.

【答案】(1)详见解析;(2)存在,2![]() +4;(3)当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
+4;(3)当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
【解析】
试题
(1)由旋转的性质结合△ABC是等边三角形可得∠DCB=60°,CD=CE,从而可得△CDE是等边三角形;
(2)由(1)可知△CDE是等边三角形,由此可得DE=CD,因此当CD⊥AB时,CD最短,则DE最短,结合△ABC是等边三角形,AC=4即可求得此时DE=CD=![]() ;
;
(3)由题意需分0≤t<6,6<t<10和t>10三种情况讨论,①当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,由此可知:此时若△DBE是直角三角形,则∠BED=90°;②当6<t<10s时,由性质的性质可知∠DBE=120°>90°,由此可知:此时△DBE不可能是直角三角形;③当t>10s时,由旋转的性质可知,∠DBE=60°,结合∠CDE=60°可得∠BDE=∠CDE+∠BDC=60°+∠BDC>60°,由此可得∠BED<60°,由此可知此时若△BDE是直角三角形,则只能是∠BDE=90°;这样结合已知条件即可分情况求出对应的t的值了.
试题解析:
(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
(2)存在,当6<t<10时,
由(1)知,△CDE是等边三角形,
∴DE=CD,
由垂线段最短可知,当CD⊥AB时,CD最小,
此时∠ADC=90°,又∵∠ACD=60°,
∴∠ACD=30°,
∴ AD=![]() AC=2,
AC=2,
∴ CD=![]() ,
,
∴ DE=2![]() (cm);
(cm);

(3)存在,理由如下:
①当0s≤t<6s时,由旋转可知,∠ABE=60°,∠BDE<60°,
∴此时若△DBE是直角三角形,则∠BED=90°,
由(1)可知,△CDE是等边三角形,
∴∠DEC=60°,
∴∠CEB=∠BED-∠DEC=30°,
∴∠CDA=∠CEB=30°,
∵∠CAB=60°,
∴∠ACD=∠ADC=30°,
∴DA=CA=4,
∴OD=OA﹣DA=6﹣4=2,
∴t=2÷1=2(s);
②当6s<t<10s时,由性质的性质可知∠DBE=120°>90°,
∴此时△DBE不可能是直角三角形;
③当t>10s时,由旋转的性质可知,∠DBE=60°,
又由(1)知∠CDE=60°,
∴∠BDE=∠CDE+∠BDC=60°+∠BDC,
而∠BDC>0°,
∴∠BDE>60°,
∴只能∠BDE=90°,
从而∠BCD=30°,
∴BD=BC=4,
∴OD=14cm,
∴t=14÷1=14(s);
综上所述:当t=2s或14s时,以D、E、B为顶点的三角形是直角三角形.

 名校课堂系列答案
名校课堂系列答案