��Ŀ����
����Ŀ����֪����![]() ���������ѧ֪ʶ̽���ú�����ͼ������ʹ������£�
���������ѧ֪ʶ̽���ú�����ͼ������ʹ������£�
��1���ú����Ա�����ȡֵ��ΧΪ��
��2���±��г�y��x�ļ����Ӧֵ������ƽ��ֱ������ϵ��������и��㣬����������ͼ��
x | �� |
|
| -1 |
| 2 |
|
| �� |
y | �� | 3 | 2 | 1 |
|
|
|
| �� |

��3�������������ͼ����������⣺
��д���ú���ͼ���һ�����ʣ���
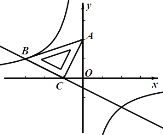
�ںᡢ�������Ϊ�����ĵ��Ϊ���㣬��ֱ��y= -x+b��ͼ�����ͼ���ཻ�γɵķ��ͼ�Σ������߽磩�ڸպ���6�����㣬��b��ȡֵ��ΧΪ��
���𰸡���1����x��-2����2������⣻��3���ٵ�x��-2ʱ��y��x�����Ӷ���С����2��b��3��
��������
��1��x+2��0��������⣻
��2����㻭������ͼ�ɣ�
��3��������д��һ�����ʼ��ɣ��ʴ𰸲�Ψһ��
����ͼ2����b=2ʱ��ֱ��y=-x+b��ͼ�����ͼ���ཻ�γɵķ��ͼ�Σ������߽磩�ڸպ���6�����㣨ͼ�п��ĵ㣩���������
�⣺��1��x+2��0����ã�x��-2��
�ʴ�Ϊ��x��-2��
��2����㻭������ͼ�����£�

��3���ٵ�x��-2ʱ��y��x�����Ӷ���С���𰸲�Ψһ����
�ʴ�Ϊ����x��-2ʱ��y��x�����Ӷ���С���𰸲�Ψһ����
����ͼ2����b=2ʱ��
ֱ��y=-x+b��ͼ�����ͼ���ཻ�γɵķ��ͼ�Σ������߽磩�ڸպ���6�����㣨ͼ�п��ĵ㣩��

��2��b��3��
�ʴ�Ϊ��2��b��3��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�