题目内容
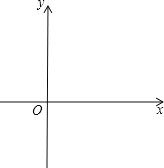
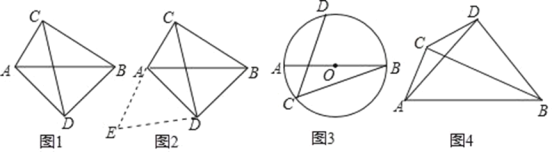
【题目】(问题背景)如图1,在四边形ADBC中,∠ACB=∠ADB=90o,AD=BD, 探究线段AC,BC,CD之间的数量关系
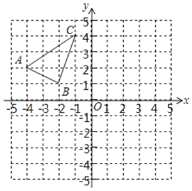
小明同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90o到△AED处,点B,C分别 落在点A,E处(如图2),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC= ![]() CD
CD
(简单应用)
(1)在图1中,若AC=6,CD=![]() ,则AB= .
,则AB= .
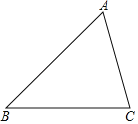
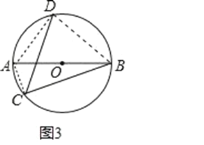
(2)如图3,AB是⊙O的直径,点C.D在⊙O上,∠C=45o,若AB=25,BC=24,求CD的长.
(拓展延伸)
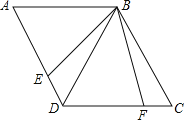
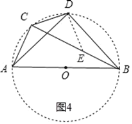
(3)如图4,∠ACB=∠ADB=90o,AD=BD,若AC=![]() ,CD=
,CD=![]() ,求BC的长.(用含
,求BC的长.(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
【答案】(1)10;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用题中结论先计算出BC=8,然后根据勾股定理计算AB的长;
(2)如图3,连接AC,AD,BD,根据圆周角定理得到∠ACB=90°,再根据勾股定理计算出AC=7,再证明AD=BD,则可利用题中结论求出CD;
(3)根据圆周角定理可判断点C、D在以AB为直径的⊙O上,再利用DA=DB得到∠DCB=∠DAB=45°,所以∠ACD=135°,作DE⊥CD交BC于E,如图4,则△CDE为等腰直角三角形,所以CE= ![]() CD=
CD=![]() ,,然后证明△ACD≌△BED得到BE=AC=a,于是有BC=CE+BE=
,,然后证明△ACD≌△BED得到BE=AC=a,于是有BC=CE+BE=![]() .
.
(1)∵AC+BC=![]() CD∴6+BC=
CD∴6+BC=![]() ×
×![]() ,∴BC=8,∴AB=10
,∴BC=8,∴AB=10
(2)如图3,连接AC,AD,BD,
∵AB为直径,∴∠ACB=90o,
∴AC= ![]()
∵∠BCD=45,
∴∠ACD=∠BCD=45o,
∴AD=BD,
∴AC+BC=![]() CD, 即7+24=
CD, 即7+24=![]() CD,
CD,
∴CD=![]()
(3)∵∠ACB=∠ADB=90o,∴点C.D在以AB为直径的⊙O上,
∵DA=DB,∴∠DAB=45,∴∠DCB=∠DAB=45o,∴∠ACD=135o,
作DE⊥CD交BC于E,如图4,
∴△CDE为等腰直角三角形,
∴CE= ![]() CD=
CD=![]() ,∠CED=45o,
,∠CED=45o,
∴∠BED=135,
在△ACD和△BED中
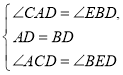
∴△ACD≌△BED(ASA),
∴BE=AC=a,∴BC=CE+BE=![]()

 天天向上口算本系列答案
天天向上口算本系列答案【题目】为了解今年我校初三学生中考体育测试成绩,现对今年我校初三中考体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中C组所在的扇形的圆心角为36°,组别成绩(分)频数.
组别 | 成绩(分) | 频数 |
A | 30<x≤34 | 1 |
B | 34<x≤38 | 1 |
C | 38<x≤42 | 6 |
D | 42<x≤46 | b |
E | 46<x≤50 | 30 |
合计 | a | |
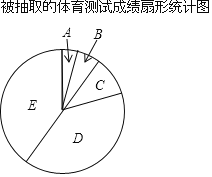
根据上面图标提供的信息,回答下列问题:
(1)计算频数分布表中a与b的值;
(2)根据C组38<x≤42的组中间值40,估计C组中所有数据的和为 ;
(3)请估计今年我校初三学生中考体育成绩的平均分(结果取整数).