题目内容
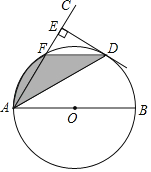
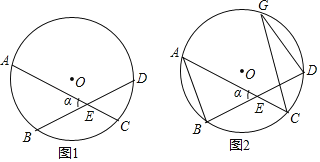
【题目】如图1,圆O的两条弦AC、BD交于点E,两条弦所成的锐角或者直角记为∠α
(1)点点同学通过画图和测量得到以下近似数据:
| 30.2° | 40.4° | 50.0° | 61.6° |
| 55.7° | 60.4° | 80.2° | 100.3° |
∠α的度数 | 43.0° | 50.2° | 65.0° | 81.0° |
猜想:![]() 、
、![]() 、∠α的度数之间的等量关系,并说明理由﹒
、∠α的度数之间的等量关系,并说明理由﹒
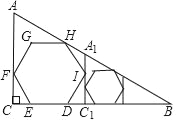
(2)如图2,若∠α=60°,AB=2,CD=1,将以![]() 圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
①求弦CG的长;
②求圆O的半径.
【答案】(1)∠α=![]() (
(![]() 的度数+
的度数+![]() 的度数),见解析;(2)①
的度数),见解析;(2)①![]() ,②
,②![]()
【解析】
(1)连接BC,如图1,先利用三角形外角性质得到∠α=∠B+∠C,再利用圆周角与它所对弧的度数之间的关系得到∠B=![]() 的度数,∠C=
的度数,∠C=![]() 的度数,所以∠α=
的度数,所以∠α=![]() (
(![]() 的度数+
的度数+![]() 的度数);
的度数);
(2)①连接OG、OC、AG,作OH⊥CG于H,GF⊥CD于F,如图2,利用旋转的性质得![]() ,AB=DG=2,利用由(1)的结论得到
,AB=DG=2,利用由(1)的结论得到![]() 的度数为120°,则∠COG=120°,
的度数为120°,则∠COG=120°,
关键圆周角定理计算出∠CDG=120°,则∠GDF=60°,于是通过解直角三角形可计算出CG的长;
②利用垂径定理得到CH=GH=![]() ,然后通过解直角三角形求出OG即可.
,然后通过解直角三角形求出OG即可.
解:(1)∠α=![]() (
(![]() 的度数+
的度数+![]() 的度数)
的度数)
理由如下:连接BC,如图1,
∠α=∠B+∠C,
而∠B=![]() 的度数,∠C=
的度数,∠C=![]() 的度数,
的度数,
∴∠α=![]() (
(![]() 的度数+
的度数+![]() 的度数);
的度数);
(2)①连接OG、OC、AG,作OH⊥CG于H,GF⊥CD于F,如图2,
∵将![]() 以圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点G,
以圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点G,
∴![]() ,AB=DG=2,
,AB=DG=2,
由(1)得![]() 的度数+
的度数+![]() 的度数=2∠α=120°,
的度数=2∠α=120°,
![]() 的度数+
的度数+![]() 的度数=2∠α=120°,
的度数=2∠α=120°,
即![]() 的度数为120°,
的度数为120°,
∴∠COG=120°,
∴∠CAG=60°,
而∠CAG+∠CDG=120°,
∴∠CDG=120°,
∴∠GDF=60°,
在Rt△GDF中,DF=![]() DG=1,GF=
DG=1,GF=![]() DF=
DF=![]() ,
,
在Rt△CFG中,CG![]() ;
;
②∵OH⊥CG,
∴CH=GH=![]() CG=
CG=![]() ,
,
∵∠OGH=![]() (180°﹣120°)=30°,
(180°﹣120°)=30°,
∴![]() ,
,
∴OG=2OH=![]() ,
,
即圆O的半径为![]() .
.

【题目】某商家销售某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x元/件满足一次函数的关系,部分数据如下表:(![]() ,物价部门规定售价不得高于80元)
,物价部门规定售价不得高于80元)
销售单价x(元/件) | … | 55 | 60 | 65 | 70 | 75 |
一周的销售量y(件) | … | 450 | 400 | 350 | 300 | 250 |
(1)直接写出y与x的函数关系式:______;
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并求出销售利润的最大值;
(3)该商家要使每周的销售利润不低于5000元,那么销售单价应控制在什么范围内?