Question

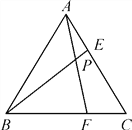
【题目】如图，等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P，且AE=CF.

(1)求证：AF=BE，并求∠FPB的度数；

(2)若AE=2，试求AP·AF的值．

Answer 1

【答案】(1)证明见解析；（2）12.

【解析】解：(1)∵△ABC为等边三角形，∴AB＝AC，∠C＝∠CAB＝60°，又∵AE＝CF，∴△ABE≌△CAF(SAS)，∴AF＝BE，∠ABE＝∠CAF.又∵∠APE＝∠BPF＝∠ABP＋∠BAP，∴∠APE＝∠BAP＋∠CAF＝60°，∴∠APB＝180°－∠APE＝120°　(2)∵∠C＝∠APE＝60°，∠PAE＝∠CAF，∴△APE∽△ACF，∴＝，即＝，∴AP·AF＝12