ЬтФПФкШн
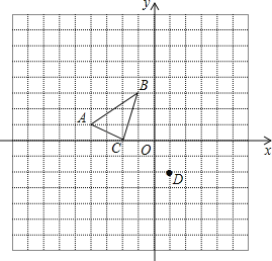
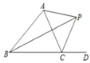
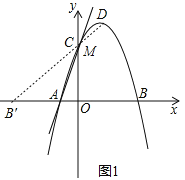
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+2x+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЪЧИУХзЮяЯпЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭжБЯпACЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧыдкyжсЩЯеввЛЕуMЃЌЪЙЁїBDMЕФжмГЄзюаЁЃЌЧѓГіЕуMЕФзјБъЃЛ
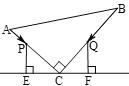
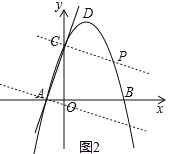
ЃЈ3ЃЉЪдЬНОПЃКдкЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙвдЕуAЃЌPЃЌCЮЊЖЅЕуЃЌACЮЊжБНЧБпЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпНтЮіЪНЮЊy=Љx2+2x+3ЃЛжБЯпACЕФНтЮіЪНЮЊy=3x+3ЃЛЃЈ2ЃЉЕуMЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЛ
ЃЈ3ЃЉЗћКЯЬѕМўЕФЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁОНтЮіЁПЃЈ1ЃЉЩшНЛЕуЪНy=aЃЈx+1ЃЉЃЈx-3ЃЉЃЌеЙПЊЕУЕН-2a=2ЃЌШЛКѓЧѓГіaМДПЩЕУЕНХзЮяЯпНтЮіЪНЃЛдйШЗЖЈCЃЈ0ЃЌ3ЃЉЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓжБЯпACЕФНтЮіЪНЃЛ
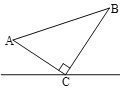
ЃЈ2ЃЉРћгУЖўДЮКЏЪ§ЕФаджЪШЗЖЈDЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌзїBЕуЙигкyжсЕФЖдГЦЕуBЁфЃЌСЌНгDBЁфНЛyжсгкMЃЌШчЭМ1ЃЌдђBЁфЃЈ-3ЃЌ0ЃЉЃЌРћгУСНЕужЎМфЯпЖЮзюЖЬПЩХаЖЯДЫЪБMB+MDЕФжЕзюаЁЃЌдђДЫЪБЁїBDMЕФжмГЄзюаЁЃЌШЛКѓЧѓГіжБЯпDBЁфЕФНтЮіЪНМДПЩЕУЕНЕуMЕФзјБъЃЛ
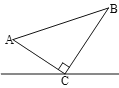
ЃЈ3ЃЉЙ§ЕуCзїACЕФДЙЯпНЛХзЮяЯпгкСэвЛЕуPЃЌШчЭМ2ЃЌРћгУСНжБЯпДЙжБвЛДЮЯюЯЕЪ§ЛЅЮЊИКЕЙЪ§ЩшжБЯпPCЕФНтЮіЪНЮЊy=-![]() x+bЃЌАбCЕузјБъДњШыЧѓГіbЕУЕНжБЯпPCЕФНтЮіЪНЮЊy=-
x+bЃЌАбCЕузјБъДњШыЧѓГіbЕУЕНжБЯпPCЕФНтЮіЪНЮЊy=-![]() x+3ЃЌдйНтЗНГЬзщ
x+3ЃЌдйНтЗНГЬзщ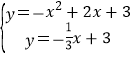 ЕУДЫЪБPЕузјБъЃЛЕБЙ§ЕуAзїACЕФДЙЯпНЛХзЮяЯпгкСэвЛЕуPЪБЃЌРћгУЭЌбљЕФЗНЗЈПЩЧѓГіДЫЪБPЕузјБъЃЎ
ЕУДЫЪБPЕузјБъЃЛЕБЙ§ЕуAзїACЕФДЙЯпНЛХзЮяЯпгкСэвЛЕуPЪБЃЌРћгУЭЌбљЕФЗНЗЈПЩЧѓГіДЫЪБPЕузјБъЃЎ
ЃЈ1ЃЉЩшХзЮяЯпНтЮіЪНЮЊy=aЃЈx+1ЃЉЃЈxЉ3ЃЉЃЌ
МДy=ax2Љ2axЉ3aЃЌ
ЁрЉ2a=2ЃЌНтЕУa=Љ1ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊy=Љx2+2x+3ЃЛ
ЕБx=0ЪБЃЌy=Љx2+2x+3=3ЃЌдђCЃЈ0ЃЌ3ЃЉЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊy=px+qЃЌ
АбAЃЈЉ1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉДњШыЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊy=3x+3ЃЛ
ЃЈ2ЃЉЁпy=Љx2+2x+3=ЉЃЈxЉ1ЃЉ2+4ЃЌ
ЁрЖЅЕуDЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌ
зїBЕуЙигкyжсЕФЖдГЦЕуBЁфЃЌСЌНгDBЁфНЛyжсгкMЃЌШчЭМ1ЃЌдђBЁфЃЈЉ3ЃЌ0ЃЉЃЌ
ЁпMB=MBЁфЃЌ
ЁрMB+MD=MBЁф+MD=DBЁфЃЌДЫЪБMB+MDЕФжЕзюаЁЃЌ
ЖјBDЕФжЕВЛБфЃЌ
ЁрДЫЪБЁїBDMЕФжмГЄзюаЁЃЌ
взЕУжБЯпDBЁфЕФНтЮіЪНЮЊy=x+3ЃЌ
ЕБx=0ЪБЃЌy=x+3=3ЃЌ
ЁрЕуMЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЛ
ЃЈ3ЃЉДцдкЃЎ
Й§ЕуCзїACЕФДЙЯпНЛХзЮяЯпгкСэвЛЕуPЃЌШчЭМ2ЃЌ
ЁпжБЯпACЕФНтЮіЪНЮЊy=3x+3ЃЌ
ЁржБЯпPCЕФНтЮіЪНПЩЩшЮЊy=Љ![]() x+bЃЌ
x+bЃЌ
АбCЃЈ0ЃЌ3ЃЉДњШыЕУb=3ЃЌ
ЁржБЯпPCЕФНтЮіЪНЮЊy=Љ![]() x+3ЃЌ
x+3ЃЌ
НтЗНГЬзщ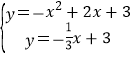 ЃЌНтЕУ
ЃЌНтЕУ![]() Лђ
Лђ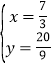 ЃЌдђДЫЪБPЕузјБъЮЊЃЈ
ЃЌдђДЫЪБPЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
Й§ЕуAзїACЕФДЙЯпНЛХзЮяЯпгкСэвЛЕуPЃЌжБЯпPCЕФНтЮіЪНПЩЩшЮЊy=Љ![]() x+bЃЌ
x+bЃЌ
АбAЃЈЉ1ЃЌ0ЃЉДњШыЕУ![]() +b=0ЃЌНтЕУb=Љ
+b=0ЃЌНтЕУb=Љ![]() ЃЌ
ЃЌ
ЁржБЯпPCЕФНтЮіЪНЮЊy=Љ![]() xЉ
xЉ![]() ЃЌ
ЃЌ
НтЗНГЬзщ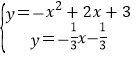 ЃЌНтЕУ
ЃЌНтЕУ![]() Лђ
Лђ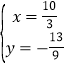 ЃЌдђДЫЪБPЕузјБъЮЊЃЈ
ЃЌдђДЫЪБPЕузјБъЮЊЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉ.
ЃЉ.
злЩЯЫљЪіЃЌЗћКЯЬѕМўЕФЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉ.
ЃЉ.

 ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ