题目内容
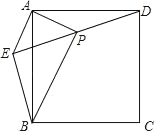
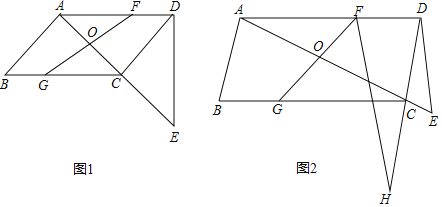
【题目】如图,在平行四边形ABCD中,AB⊥AC,过点D作DE⊥AD交直线AC于点E,点O是对角线AC的中点,点F是线段AD上一点,连接FO并延长交BC于点G.
(1)如图1,若AC=4,cos∠CAD=![]() ,求△ADE的面积;
,求△ADE的面积;
(2)如图2,点H为DC是延长线上一点,连接HF,若∠H=30°,DE=BG,求证:DH=CE+![]() FH.
FH.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)根据平行四边形的性质得到∠CAD=∠ACB,因为AB⊥AC,根据三角函数得到cos∠CAD![]() ,cos∠CAD=
,cos∠CAD=![]() ,再根据勾股定理进行计算即可得到答案;
,再根据勾股定理进行计算即可得到答案;
(2)作FK⊥DH于K,根据题意,由三角函数得到HK=![]() FH,根据全等三角形的判定(ASA)得到△BOG≌△DOF(ASA),根据全等三角形的性质得到BG=DF,结合题意根据全等三角形的判定(AAS)和性质即可得到答案.
FH,根据全等三角形的判定(ASA)得到△BOG≌△DOF(ASA),根据全等三角形的性质得到BG=DF,结合题意根据全等三角形的判定(AAS)和性质即可得到答案.
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠CAD=∠ACB,
∵AB⊥AC,
∴cos∠CAD=![]() =cos∠ACB=
=cos∠ACB=![]() =
=![]() ,
,
∴BC=AD=5,
∵cos∠CAD=![]() ,
,
∴![]() =
=![]() ,
,
∴AE=![]() ,
,
DE=![]() =
=![]() =
=![]() ,
,
S△ADE=![]() ADDE=
ADDE=![]() ×5×
×5×![]() =
=![]() ;
;
(2)证明:作FK⊥DH于K,如图2所示:

∵∠H=30°,
∴∠HFK=60°,
∴HK=sin60°FH=![]() FH,
FH,
连接BD,则OB=OD,∠OBG=∠ODF,∠BOG=∠DOF,
在△BOG和△DOF中,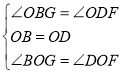 ,
,
∴△BOG≌△DOF(ASA),
∴BG=DF,
∵DE=BG,
∴DE=DF,
∵AB⊥AC,AB∥CD,
∴CD⊥AC,
∴∠DCE=∠FKD=90°,
∵∠CDE+∠CED=90°,∠CDE+∠KDF=90°,
∴∠CED=∠KDF,
在△DCE和△FKD中,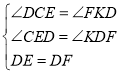 ,
,
∴△DCE≌△FKD(AAS),
∴DK=CE,
∴DH=DK+HK=CE+![]() FH.
FH.

【题目】某区规定学生每天户外体育活动时间不少于1小时.为了解学生参加户外体育活动的情况,对部分学生每天参加户外体育活动的时间进行了随机抽样调查,并将调查结果绘制成如下的统计表(不完整).

组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t<0.5 | 20 | 0.05 |
B | 0.5≤t<1 | a | 0.3 |
C | 1≤t<1.5 | 140 | 0.35 |
D | 1.5≤t<2 | 80 | 0.2 |
E | 2≤t<2.5 | 40 | 0.1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,将频数分布直方图补全;
(2)该区8000名学生中,每天户外体育活动的时间不足1小时的学生大约有多少名?
(3)若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名,请用画树状图或列表法求恰好抽到1名男生和1名女生的概率.