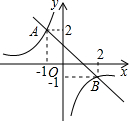题目内容
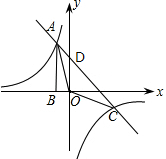
点A是双曲线y=
与直线y=-x-(k+1)在第二象限的交点,AB垂直x轴于点B,且S△ABO=
;
(1)求两个函数的表达式;
(2)求直线与双曲线的交点坐标和△AOC的面积.
| k |
| x |
| 3 |
| 2 |
(1)求两个函数的表达式;
(2)求直线与双曲线的交点坐标和△AOC的面积.

(1)设A点坐标为(x,y),且x<0,y>0,
则S△ABO=
•|BO|•|BA|=
•(-x)•y=
,
∴xy=-3,
又∵y=
,
即xy=k,
∴k=-3,
∴所求的两个函数的解析式分别为y=-
,y=-x+2;
(2)由y=-x+2,
令x=0,得y=2.
∴直线y=-x+2与y轴的交点D的坐标为(0,2),
A、C两点坐标满足
,
解得x1=-1,y1=3,x2=3,y2=-1,
∴交点A为(-1,3),C为(3,-1),
∴S△AOC=S△ODA+S△ODC=
•|OD|•(|y1|+|y2|)=
×2×(3+1)=4.
则S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴xy=-3,
又∵y=
| k |
| x |
即xy=k,
∴k=-3,
∴所求的两个函数的解析式分别为y=-
| 3 |
| x |
(2)由y=-x+2,
令x=0,得y=2.
∴直线y=-x+2与y轴的交点D的坐标为(0,2),
A、C两点坐标满足
|
解得x1=-1,y1=3,x2=3,y2=-1,
∴交点A为(-1,3),C为(3,-1),
∴S△AOC=S△ODA+S△ODC=
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
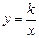 的图象经过点A(1,3).
的图象经过点A(1,3). 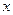 =2时, 求y的值;
=2时, 求y的值; 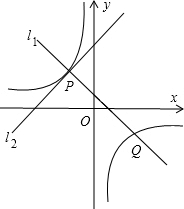 线
线 —
—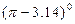 +
+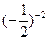
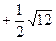
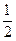 时,y的值.
时,y的值.