题目内容
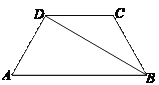
【题目】如图,在等腰梯形ABCD中,DC∥AB,AD=BC=2,BD平分∠ABC.∠A=60°,求对角线BD的长和梯形ABCD的面积.
【答案】2![]() ,3
,3![]()
【解析】分析:过点D作DH⊥AB,垂足为H.利用等腰梯形的性质证△ABD与△DBH均为含30度角的直角三角形,即可求出AB、BD、DH的长,再利用平行及角平分线证明△BCD为等腰三角形即可得出DC的长,最后利用梯形的面积公式求解即可.
详解:过点D作DH⊥AB,垂足为H.
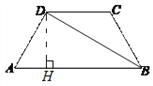
在等腰梯形ABCD中,
∵∠A=60°,
∴∠ABC=∠A=60°,
∵BD平分∠ABC,
∴∠ABD=∠CBD =30°,
在△ABD中,
∵∠A+∠ABD+∠ADB=180°,
∴∠ADB=90°
∴AD=![]() AB,
AB,
∵AD=2,
∴AB=4.
∴由勾股定理BD=![]() ,
,
在Rt△BDH中,
∵∠DBH=30°,
∴DH=![]() BD=
BD=![]() ,
,
∵DC∥AB,
∴∠ABD=∠CDB,
又∵∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴CD=BC=2,
∴![]() .
.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目