题目内容
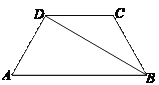
【题目】如图，在平行四边形ABCD中，∠ABC=45°，E、F分别在CD和BC的延长线上，AE∥BD，∠EFC=30°， AB=2.
求CF的长．
【答案】2
+2
．
【解析】
试题分析：易证四边形ABDE是平行四边形，则AB=DE=CD，过点E作EH⊥BF于点H，解等腰直角三角形CEH得EH=CH=2，解FH=2，从而得CF=2+2．
试题解析：∵四边形ABCD是平行四边形，∴AB∥DC，AB=DC.
∵AE∥BD，∴四边形ABDE是平行四边形.
∴AB=DE=CD，即D为CE中点.
∵AB=2，∴CE=4.
又∵AB∥CD，∴∠ECF=∠ABC=45°.
如图，过点E作EH⊥BF于点H，
∵CE=4，∠ECF=45°，∴EH=CH=2.
∵∠EFC=30°，∴ FH=2，∴ CF=2+2．
练习册系列答案
相关题目
