题目内容
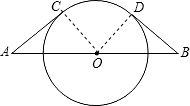
如图，AB=6
，O为AB的中点，AC，BD都是半径为3的⊙O的切线，C，D为切点，则
的长为（ ）
| 2 |
 |
| CD |
A．
| B．
| C．3
| D．3π |
连接OC，OD，
∵AC，BD都是半径为3的⊙O的切线，
∴OC⊥AC，OD⊥BD，且OC=OD=3，
∵AB=6
，O为AB的中点，
∴OA=OB=3
，
∴cos∠AOC=cos∠BOD=
=
，
∴∠AOC=∠BOD=45°，
∴∠COD=180°-∠AOC-∠BOC=90°，
∴
的长为：
=
π．
故选A．
∵AC，BD都是半径为3的⊙O的切线，
∴OC⊥AC，OD⊥BD，且OC=OD=3，
∵AB=6
| 2 |
∴OA=OB=3
| 2 |
∴cos∠AOC=cos∠BOD=
| 3 | ||
3
|
| ||
| 2 |
∴∠AOC=∠BOD=45°，
∴∠COD=180°-∠AOC-∠BOC=90°，
∴
|
| CD |
| 90×π×3 |
| 180 |
| 3 |
| 2 |
故选A．
练习册系列答案
提分百分百检测卷系列答案
相关题目
，垂足为F．
