Question

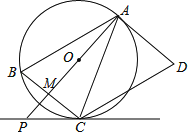
【题目】如图所示，AB是⊙O的直径，AM、BN是⊙O的两条切线，D、C分别在AM、BN上，DC切⊙O于点E，连接OD、OC、BE、AE，BE与OC相交于点P，AE与OD相交于点Q，已知AD=4，BC=9，以下结论：

①⊙O的半径为 ，②OD∥BE ，③PB=， ④tan∠CEP=

其中正确结论有（ ）

A.1个B.2个C.3个D.4个

Answer 1

【答案】C

【解析】

试题解析：作DK⊥BC于K，连接OE．

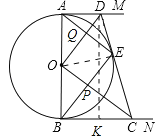
∵AD、BC是切线，∴∠DAB=∠ABK=∠DKB=90°，∴四边形ABKD是矩形，∴DK=AB，AD=BK=4，∵CD是切线，∴DA=DE，CE=CB=9，在RT△DKC中，∵DC=DE+CE=13，CK=BC﹣BK=5，∴DK==12，∴AB=DK=12，∴⊙O半径为6．故①错误，∵DA=DE，OA=OE，∴OD垂直平分AE，同理OC垂直平分BE，∴AQ=QE，∵AO=OB，∴OD∥BE，故②正确．

在RT△OBC中，PB===，故③正确，∵CE=CB，∴∠CEB=∠CBE，∴tan∠CEP=tan∠CBP===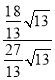，故④正确，∴②③④正确，故选C．