Question

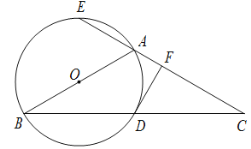
【题目】如图，已知∠ACB＝90°，AC＞BC，分别以△ABC的边AB，BC，CA为一边向△ABC外作正方形ABDE，正方形BCMN，正方形CAFG，连接EF，GM，设△AEF，△CGM的面积分别为S1，S2，则下列结论正确的是（　　）

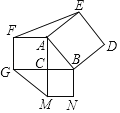
A.S1＝S2B.S1＜S2C.S1＞S2D.S1≤S2

Answer 1

【答案】A

【解析】

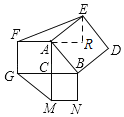
设直角三角形的三边分别为a、b、c，过E作ER⊥AF，交FA的延长线于R，分别表示出△AEF，△CGM的面积，进行比较即可．

过E作ER⊥AF，交FA的延长线于R，

设△ABC的三边BC，AC，AB的长分别为a、b、c，

∵分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG，

∴AE＝AB，∠ARE＝∠ACB＝90°，

∵∠EAR+∠BAR＝∠BAR+∠CAB=90°，

∴∠EAR=∠CAB，

∴△AER≌△ABC（AAS），

∴ER＝BC＝a，

∵FA＝b，

∴S1＝ab，

∵CG＝b，CM＝a，

∴S2＝ab，

∴S1＝S2，

故选：A．