题目内容
【题目】如图,在矩形OABC中,OA=5,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
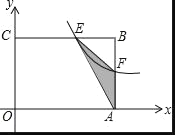
(1)当F为AB的中点时,求该函数的表达式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
【答案】(1)y=![]() ;(2)当k=10时,S△EFA有最大值,S最大值=
;(2)当k=10时,S△EFA有最大值,S最大值=![]() .
.
【解析】
(1)当F为AB的中点时,点F的坐标为(5,2),由此代入求得函数解析式即可;
(2)根据图中的点的坐标表示出三角形的面积,得到关于k的二次函数,利用二次函数求出最值即可.
解:(1)∵在矩形OABC中,OA=5,OC=4,
∴B(5,4),
∵F为AB的中点,
∴F(5,2),
∵点F在反比例函数y=![]() 的图象上,
的图象上,
∴k=10,
∴该函数的解析式为y=![]()
![]() ;
;
(2)由题意知E,F两点坐标分别为E(![]() ,4),F(5,
,4),F(5,![]() ),
),
∵S△EFA=![]() AFBE=
AFBE=![]() ×
×![]() (5-
(5-![]() )=-
)=-![]() k2+
k2+![]() =-
=-![]() (k﹣10)2+
(k﹣10)2+![]() ,
,
∴当k=10时,S△EFA有最大值,S最大值=![]() .
.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?