题目内容
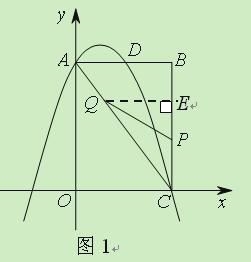
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
【答案】解:(1)将A、C两点坐标代入抛物线![]() ,
,
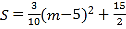 ,
,
解得![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)①∵OA=8,OC=6
∴![]() ,
,
过点Q作QE⊥BC与E点,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴当m=5时,S取最大值;
②在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
满足条件的点F共有四个,坐标分别为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
【解析】
略

练习册系列答案
相关题目