题目内容
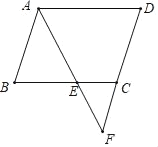
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.
(1)若AB=4,BC=6,求EC的长;
(2)若∠EAD=50°,求∠BAE和∠D的度数.
【答案】(1)2;(2)∠BAE=50°,∠D=80°.
【解析】
(1)利用平行四边形的性质以及平行线的性质得出∠AEB=∠BAE,进而得出AB=BE,由此即可求得EC的长;(2)利用角平分线定义和平行线的性质即可解答.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠AEB,
又∵AE平分∠BAD,
∴∠DAF=∠BAE,
∴∠AEB=∠BAE,
∴AB=BE=4,
∴EC=BC﹣BE=6﹣4=2;
(2)∵∠EAD=50°,AE平分∠BAD,
∴∠BAE=50°,
∴∠BAD=100°,
∵AB∥CD,
∴∠D+∠BAD=180°,
∴∠D=180°﹣100°=80°.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目