题目内容
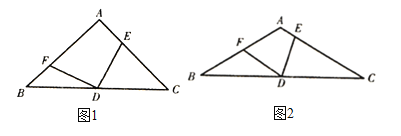
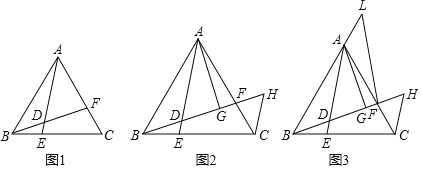
【题目】△ABC是等边三角形,点E、F分别是边BC、AC上的点,且BE=CF,AE、BF交于点D.
(1)如图1,求证:AE=BF.
(2)如图2,过点A作AG⊥BF于点G,过点C作CH∥AE交BF延长线于点H,若D为BG中点,求BH:CH的值;
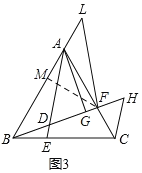
(3)如图3,在(2)的条件下,L为BA延长线上一点,且FL=FB,△FLA的面积为2,求△ABC的面积.
【答案】(1)证明见解析;(2)BH:CH=![]() ;(3)△ABC的面积为9.
;(3)△ABC的面积为9.
【解析】
(1)根据等边三角形的性质得到AB=BC,∠ABC=∠C,证明△ABE≌△BCF,根据全等三角形的性质,得到答案;
(2)连接CG,证明△ABD≌△BCG(SAS),得BD=CG,∠ADB=∠BGC=120![]() ,根据平行线的性质得∠H=∠ADG=60
,根据平行线的性质得∠H=∠ADG=60![]() ,证明△CGH是等边三角形,得BH=3BD=3CH,得结论;
,证明△CGH是等边三角形,得BH=3BD=3CH,得结论;
(3)如图3,作辅助线,构建高线FM,设CF=a,证明△BCF∽△BHC,![]() ,根据同高三角形面积的比为对应底边的比.
,根据同高三角形面积的比为对应底边的比.
(1)如图1.
∵三角形ABC是等边三角形,

∴AB=BC,∠ABE=∠BCF=60![]() ,
,
在△ABE和△BCF中,
 ,
,
∴△ABE≌△BCF(SAS),
∴AE=BF;
(2)如图2,由(1)得:△ABE≌△BCF,
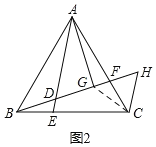
∴∠BAE=∠CBF.
∵∠ADG=∠ABD+∠BAE,
∴∠ADG=∠ABD+∠CBF=∠ABC=60![]() ,
,
∴∠ADB=120![]() .
.
∵AG⊥BH,
∴∠DAG=30![]() ,
,
∴DG=![]() AD.
AD.
∵D为BG中点,
∴BD=DG=![]() BG,
BG,
∴AD=BG,
连接CG,如图2所示:
在△ABD和△BCG中,
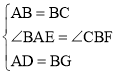 ,
,
∴△ABD≌△BCG(SAS),
∴BD=CG,∠ADB=∠BGC=120![]() ,
,
∴∠CGH=60![]() .
.
∵CH∥AE,
∴∠H=∠ADG=60![]() ,
,
∴∠CGH=∠H=60![]() ,
,
∴△CGH是等边三角形,
∴GH=CH=CG=BD,
∴BH=3BD=3CH,
∴BH:CH=![]() ;
;
(3)如图3,由(2)知:∠H=∠ADF=60![]() ,
,
∴∠BCF=∠H=60![]() ,∠CBF=∠CBH,
,∠CBF=∠CBH,
∴△BCF∽△BHC,
∴![]() ,
,
设CF=a,则BC=3a,AF=2a,
过F作FM⊥AB于M,
Rt△AFM中,∠FAM=60![]() ,∴∠AFM=30
,∴∠AFM=30![]() ,∴AM=a,FM=
,∴AM=a,FM=![]() a,
a,
∴BM=3a﹣a=2a.
∵BF=FL,
∴LM=BM=2a,
∴AL=a,
∴![]() =
=![]() .
.
∵△FLA的面积为2,
∴△ABF的面积为6.
∵![]()
∴△ABC的面积为9.